AMAZON multi-meters discounts AMAZON oscilloscope discounts
..
Laplace Transform
The Laplace transform is used to map a differential equation in the 'time domain' (i.e. involving 't') to the 'frequency domain' (involving 's'). The procedure unfolds as explained next.
First, the applied time-dependent stimulus (one-shot or repetitive - voltage or current) is mapped into the complex-frequency domain, that is, the s-plane. Then, by using the s-plane versions of the impedances, we can transform the entire circuit into the s-plane. To this transformed circuit we apply the s-plane versions of the basic electrical laws and thereby analyze the circuit. We will then need to solve the resultant (transformed) differential equation (now in terms of s rather than t). But as mentioned, we will be happy to discover that the manipulation and solution of such differential equations is much easier to do in the s-plane than in the time domain. In addition, there are also several lookup tables for the Laplace transforms of common functions available, to help along the way. We will thus get the response of the circuit in the frequency domain. Thereafter, if so desired, we can use the 'inverse Laplace transform' to recover the result in the time domain. The entire procedure is shown symbolically in Fig. 3.
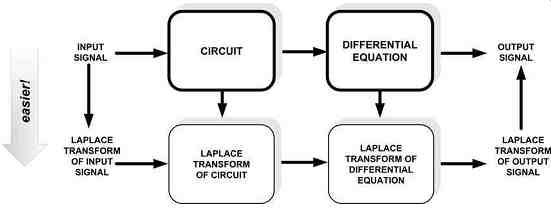
A little more math is useful at this point, as it will aid our understanding of the principles of feedback loop stability later.
Suppose the input signal (in the time domain) is u(t), and the output is v(t), and they are connected by a general second-order differential equation of the type ...
It can be shown that if U(s) is the Laplace transform of u(t), and V(s) the transform of v(t), then this equation (in the frequency domain) becomes simply ...
We can therefore define G(s), the transfer function (i.e. output divided by input in the s-plane now), as ... Therefore:
V(s) = G(s) · U(s)
Note that this is analogous to the time-domain version of a general transfer function f(t)
v(t) = f(t) · u(t)
Since the solutions for the general equation G(s) above are well researched and documented, we can easily compute the response (V) to the stimulus (U).
A power supply designer is usually interested in ensuring that his or her power supply operates in a stable manner over its operating range. To that end, a sine wave is injected at a suitable point in the power supply, and the frequency swept, to study the response.
This could be done in the lab, and/or "on paper" as we will soon see. In effect, what we are looking at closely is the response of the power supply to any frequency component of a repetitive or nonrepetitive impulse. But in doing so, we are in effect only dealing with a steady sine wave stimulus (swept). So we can put s = j? (i.e. s = 0).
We can ask - why do we need the complex s-plane at all if we are going to use s = j? anyway at the end? The answer to that is - we don't always. For example, at some later stage we may want to compute the exact response of the power supply to a specific disturbance (like a step change in line or load). Then we would need the s-plane and the Laplace transform. So, even though more often we end up just doing steady state analysis, by having already characterized the system in the framework of s, we retain the option to be able to conduct a more elaborate analysis of the system response to a more general stimulus if required.
A silver lining for the beleaguered power supply designer is that he or she usually doesn't even need to know how to actually compute the Laplace transform of a function - unless, For example, the exact step response is required to be computed exactly. Just for ensuring stability margins, it turns out that a steady state analysis serves the purpose completely. So typically, we do the initial math in the complex s-plane, but at the end, to generate the results of the margin analysis, we again revert to s = j?.
Disturbances and the Role of Feedback
In power supplies, we can either change the applied input voltage or increase the load (this may or may not be done suddenly). Either way, we always want the output to remain well regulated, and therefore, in effect, to "reject" the disturbance.
But in practice, that clearly does not happen in a perfect manner, as we may have desired.
For example, if we suddenly increase the input to a buck regulator, the output initially just tends to follow suit - since D = VO/VIN, and D has not immediately changed. To maintain output regulation, the control section of the IC needs to sense the change in the output (that may take some time), correct the duty cycle (that also may take some time), and then wait (a comparatively longer time) for the inductor and output capacitor either to give up some of their stored energy or to gather some more (whatever is consistent with the conditions required for the new steady state). Eventually, the output will hopefully settle down again.
We see that there are several such delays in the circuit before we can get the output to stabilize again. Minimizing these delays is clearly of great interest. Therefore, for example, using smaller filter components (L and C) will usually help the circuit respond faster.
However, one philosophical question still remains - how can the control circuit ever know beforehand how much correction (in duty cycle) to precisely apply (when it senses that the output has shifted from its set value on account of the disturbance)? In fact, it usually doesn't! It can only be designed to "know" what general direction to move in, but not by how much. Hypothetically speaking, we can do several things. For example, we can command the duty cycle to change slowly and progressively, with the output being monitored continuously, and stop correcting the duty cycle at the exact moment when the output returns to its regulation level. However, clearly this is a slow process, and so though the duty cycle itself won't "overshoot," the output will certainly overshoot or undershoot as the case may be, for a rather long time. Another way is to command the duty cycle to change suddenly by a large arbitrary amount (though of course in the right direction). However, now the possibility of over-correction arises, as the output could well "go the other way," before the control realizes it. And further, when it does, it may tend to "overreact" once more... and so on. In effect, we now get "ringing" at the output. This ringing reflects a basic cause-effect uncertainty that is present in any feedback loop - the control never fully knows whether the error it’s seeing, is truly a response to an external disturbance, or its own attempted correction coming back to haunt it. So, if after a lot of such ringing, the output does indeed stabilize, the converter is considered only 'marginally stable.' In the worst case, this ringing may go on forever, even escalating, before it stabilizes. In effect, the control is then "fully confused," and so the feedback loop is deemed "unstable." We see that an "optimum" feedback loop is neither too slow, nor too fast. If it’s too slow, the output will exhibit severe overshoot (or undershoot). And if it’s too fast (over-aggressive), the output may ring severely, and even break into full instability (oscillations).
The study of how any disturbance propagates inside the converter, either getting attenuated or exacerbated in the process, is called 'feedback loop analysis.' As mentioned, in practice, we test a feedback loop by deliberately injecting a small disturbance at an appropriate point inside it (cause), and then seeing at what magnitude and phase it returns to the same point (effect). If, for example, we find that the disturbance reinforces itself (at the right phase), cause-effect separation will be completely lost, and instability will result.
The very use of the word "phase" in the previous paragraph implies we are talking of sine waves once again. However, this turns out to be a valid assumption, because as we know, arbitrary disturbances can be decomposed into a series of sine wave components of varying frequencies. So the signal we "inject" (either on the bench, or on paper) can be a sine wave of constant, but arbitrary amplitude. Then, by sweeping the frequency over a wide range, we can look for frequency components (sine waves) that have the potential to lead to instability - assuming we can have a disturbance that happens to contain that particular frequency component. If the system is stable for a wide range of sine wave frequencies, it would in effect be stable when subjected to an arbitrarily-shaped disturbance too.
A word on the amplitude of the disturbance. Note that we are studying only linear systems.
That means, if the input to a two-port network doubles, so does the output. Their ratio is therefore unchanged. In fact, that is why the transfer function was never thought of as say, being a function of the amplitude of the incoming signal. But we do know that in reality, if the disturbance is too severe, parts of the control circuit may "rail" - that means for example an internal op-amp's output may momentarily reach very close to its supply rails, thus affording no further correction for some time. We also realize that there is no perfectly "linear system." However, any system can be approximated by a linear system if the stimulus (and response) is "small" enough. That is why, when we conduct feedback loop analysis of power converters, we talk in terms of 'small-signal analysis' and 'small-signal models.' Applying these facts to our injected (swept) sine wave, we realize that its amplitude should not be made too large, or else internal "railing" or "clipping" can affect the validity of our data and the conclusions. But it must not be made too small either, otherwise switching noise is bound to overwhelm the readings (poor signal to noise ratio). A power supply designer may have to struggle a bit on the bench to get the right amplitude for taking such measurements.
And that may depend on the frequency. Therefore, more advanced instruments currently available allow the user to tailor the amplitude of the injected signal with respect to the (swept) frequency. So For example, we can demand that at higher sweep frequencies, the amplitude is set lower than the amplitude at lower frequencies. If we are looking at the switching waveform on an oscilloscope, we should see a small jitter - typically about 5 to 10% around the "edge." Too small a jitter indicates the amplitude is too small, and too large a jitter can cause strange behavior, especially if we are operating very close to the "stops" - the minimum or maximum duty cycle limits of the controller, and/or the set current limit.
Transfer Function of the RC Filter
Let us now take our simple series RC network and transform it into the frequency domain, as shown in Fig. 4. As we can see, the procedure for doing this is based on the well-known equation for a dc voltage divider - now extended to the s-plane.
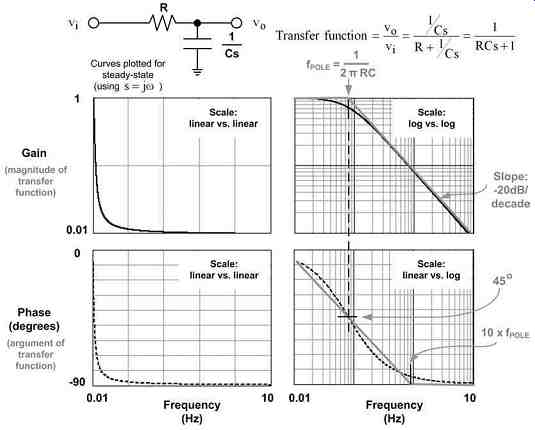
Fig. 4: Analyzing the First-order Low-pass RC Filter in the Frequency
Domain
Thereafter, since we are looking at only steady state excitations (not transient impulses), we can set s = j?, and plot out a) the magnitude of the transfer function (i.e. its 'gain'), and b) the argument of the transfer function (i.e. its phase) - both in the frequency domain of course. This combined gain-phase plot is called a 'Bode plot'.
Note that gain and phase are defined only in steady state as they implicitly refer to a sine wave ("phase" has no meaning otherwise!).
Here are a few observations:
++ In the curves of Fig. 4, we have preferred to convert the phase angle (which was originally in radians, ? = ?t), into degrees. That is because most of us feel more comfortable visualizing degrees, not radians. To do this, we have used the following conversion - degrees = (180/p) × radians.
++ We have also similarly converted from the 'angular frequency' (?) to the usual frequency (in Hz). Here we have used the equation - Hz = (radians/second)/(2p).
++ By varying the type of scaling on the gain and phase plots, we can see that the gain becomes a straight line if we use log vs. log scaling (remember that the exponential function needed log vs. linear scaling to appear as a straight line). We thus confirm by looking at these curves, that the gain at high frequencies starts decreasing by a factor of 10 for every 10-fold increase in frequency. Note that by definition, a 'decibel' or 'dB' is dB = 20 × log (ratio) - when used to express voltage or current ratios. So, a 10:1 voltage ratio is 20 dB. Therefore we can say that the gain falls at the rate of -20 decibels per decade at higher frequencies. Any circuit with a slope of this magnitude is called a 'first-order filter' (in this case a low-pass one).
++ Further, since this slope is constant, the signal must also decrease by a factor of 2 for every doubling of frequency. Or a factor of 4 for every quadrupling of frequency, and so on. But a 2:1 ratio is 6 dB, and an "octave" is a doubling (or halving) of frequency. Therefore we can also say that the gain of a low-pass first-order filter falls at the rate of -6 dB per octave (at high frequencies).
++ If the x and y scales are scaled and proportioned identically, the angle the gain plot will make with the x-axis is -45°. The slope, that is, tangent of this angle is then tan(-45°) =-1. Therefore, a slope of -20 dB/decade (or -6 dB/octave) is often simply called a "-1" slope.
++ Similarly, when we have filters with two reactive components (an inductor and a capacitor), we will find the slope is -40 dB/decade (i.e. -12 dB/octave). This is usually called a "-2" slope (the angle being about -63°).
++ We will get a straight-line gain plot in either of the two following cases - a) if the gain is expressed as a simple ratio (i.e. Vout/Vin), and plotted on a log scale (on the y-axis), or b) if the gain is expressed in decibels (i.e. 20 × log Vout/Vin), and we use a linear scale to plot it. Note that in both cases, on the x-axis, we can either use "f" (frequency) on a log scale, or 20 × log (f) on a linear scale.
++ We must remember that the log of 0 is indeterminate (log 0 ?-8), so we must not let the origin of a log scale ever be 0. We can set it close to zero, say 0.0001, or 0.001, or 0.01, and so on, but certainly not 0.
++ The bold gray straight lines in both the right-hand side graphs of Fig. 4 form the 'asymptotic approximation. 'We see that the gain asymptotes have a break frequency or 'corner frequency' at f = 1/(2pRC). This point can also be referred to as the 'resonant frequency' of the RC filter.
++ The error/deviation from the actual curve is usually very small if we replace it with its asymptotes (for first-order filters). For example, the worst-case error for the gain of the simple RC network is only -3dB, and occurs at the break frequency.
Therefore, the asymptotic approximation is a valid "short cut" that we will often use from now on to simplify the plots and their analysis.
++ With regard to the asymptotes of the phase plot, we see that we get two break frequencies for it - one at 1/10th, and the other at 10 times the break frequency of the gain plot. The change in the phase angle at each of these break points is 45° - giving a total phase shift of 90° spanning two decades (symmetrically around the break frequency of the gain plot).
++ Note that at the frequency where the single-pole lies, the phase shift (measured from the origin) is always 45° - that is, half the overall shift - whether we are using the asymptotic approximation or not.
++ Since both the gain and the phase fall as frequency increases, we say we have a 'pole' present - in our case, at the break frequency of 1/(2pRC). It’s also a "single-pole," since it’s associated with only a -1 slope.
++ Later, we will see that a 'zero' is identifiable by the fact that both the gain and phase rise with frequency.
++ The output voltage is clearly always less than the input voltage - at least for a (passive) RC network. In other words, the gain is less than 1, at any frequency.
Intuitively, that seems right, because there seems to be no way to "amplify" a signal, without using an active device - like an op-amp for example. However, as we will soon see, if we use filters that use both types of reactive components (L and C), we can in fact get the output voltage to exceed the input (but only at certain frequencies).
And that incidentally is what we more commonly regard as "resonance."
The Integrator Op-amp ("pole-at-zero" filter)
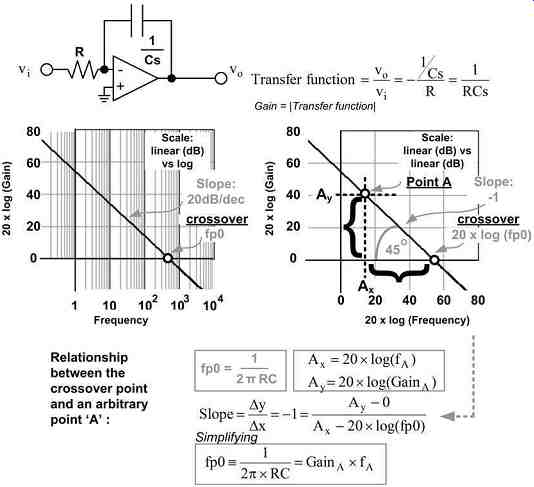
Fig. 5: The Integrator (pole-at-zero) Operational Amplifier
Before we go on to passive networks involving two reactive components, let us look at an interesting active RC based filter. The one chosen for discussion here is the 'integrator,' because it happens to be the fundamental building block of any 'compensation network.' The inverting op-amp presented in Fig. 5 has only a capacitor present in its feedback path. We know that under steady dc conditions, all capacitors essentially "go out of the picture." In our case we are therefore left with no negative feedback at all at dc - and therefore infinite dc gain (though in practice, real op-amps will limit this to a very high, but finite value). But more surprisingly perhaps, that does not stop us from knowing the precise gain at higher frequencies. If we calculate the transfer function of this circuit, we will see that something "special" again happens at the point f = 1/(2p × RC). However unlike the passive RC filter, this point is not a break-point (or a pole, or zero location). It happens to be the point where the gain is unity (0 dB). We will denote this frequency as "fp0." This is therefore the crossover frequency of the integrator. "Crossover" implies that the gain plot intersects the 0 dB (gain = 1) axis.
Note that the integrator has a single-pole -- at "zero frequency". Therefore, we will often refer to it as the "pole-at-zero" stage or section of the compensation network. This pole is more commonly called the pole at the origin or the dominant pole.
The basic reason why we will always strive to introduce this pole-at-zero is that without it we would have very limited dc gain. The integrator is the simplest way to try and get as high a dc gain as possible.
On the right side of Fig. 5, we have deliberately made the graph perfectly square in shape. We have also assigned an equal number of grid divisions on the two axes. In addition, to keep the x and y scaling identical, we have plotted 20 × log(f) on the x-axis (instead of just log(f)). Having thus made the x- and y-axes identical in all respects, we realize why the slope is called "-1" - it really does fall at exactly 45° now (visually too).
Therefore, by plotting 20 × log(gain) versus 20 × log(f), we have obtained a straight line with a -1 slope. This allows us to do some simple math as shown in Fig. 5. We have thus derived a useful relationship between an arbitrary point "A" and the crossover frequency ...
Note that in general, the transfer function of a "pole-at-zero" function such as this will always have the following form:
1/Xs (pole-at-zero transfer function) The crossover frequency is f_cross = 1/2pX (crossover frequency) In our case, X is the time constant RC.