AMAZON multi-meters discounts AMAZON oscilloscope discounts
Some of the basics of alternating current (AC) power systems were discussed in Section 2. You should already have an understanding of the effects of resistance, inductance, and capacitance in AC circuits. Therefore, this Section will deal primarily with the systems that are used to produce AC electrical power.
The vast majority of the electrical power produced in the United States is alternating current. Massive mechanical generators at power plants throughout our country provide the necessary electrical power to supply our homes and industries. Most generators produce three-phase alternating current; however, single-phase generators are also used for certain applications of a smaller nature. The operation of mechanical generators relies upon a fundamental principle of electricity called electromagnetic induction.
TERMINOLOGY
This Section (Section 6) deals with AC power systems. After studying this Section, you should have an understanding of the following terms:
- Electromagnetic Induction
- Faraday's Law
- Left-Hand Rule of Generation
- Single-Phase AC Voltage
- Generator
- Stator
- Rotor
- Field Pole
- Prime Mover
- Slip Ring/Brush Assembly
- AC Sine Wave
- Single-Phase AC Generator
- Rotating-Armature Method
- Rotating-Field Method
- Three-Phase AC Generator
- Three-Phase Wye Connection
- Three-Phase Delta Connection
- High-Speed Generator
- Low-Speed Generator
- Frequency
- Harmonics
- Voltage Regulation
- Efficiency
ELECTROMAGNETIC INDUCTION
The basic principle that allows electrical power to be produced by alternators was discovered in the early 1800s by Michael Faraday, an English scientist. Faraday's Law is the basis of electrical power production. The principle of electromagnetic induction was one of the most important discoveries in the development of modern technology. Without electrical power, our lives would certainly be different. Electromagnetic induction, as the name implies, involves electricity and magnetism.
When electrical conductors, such as alternator windings, are moved within a magnetic field, an electrical current develops in the conductors.
The electrical current produced in this way is caned an induced current. A simplified illustration showing how induced electrical current develops is shown in FIG. 1
A conductor is placed within the magnetic field of a horseshoe mag net so that the left side of the magnet has a north polarity (N), and the right side has a south polarity (S). Magnetic lines of force travel from the north polarity of the magnet to the south polarity. The ends of the conductor are connected to a current meter to measure the induced current. The meter is the zero-centered type, so its needle can move either to the left or to the right. When the conductor is moved, current will flow through the conductor. Electromagnetic induction takes place whenever there is relative motion between the conductor and the magnetic field. Either the conductor can be moved through the magnetic field, or the conductor can be held stationary and the magnetic field can be moved past it. Thus, current will be induced as long as there is relative motion between the conductor and magnetic field.
If the conductor shown in FIG. 1 is moved upward, the needle of the meter will move to the right. However, if the conductor is moved downward, the needle of the meter will deflect to the left. This shows that the direction of movement of the conductor within the magnetic field determines the direction of current flow. In one case, the current flows through the conductor from the front of the illustration to the back. In the other situation, the current travels from the back to the front. The direction of current flow is indicated by the direction of the meter deflection. The principle demonstrated here is the basis for electrical power generation.
In order for an induced current to be developed, the conductor must have a complete path or closed circuit. The meter in FIG. 1 was connected to the conductor to make a complete current path. If there is no closed circuit, electromagnetic induction cannot take place. It is important to remember that an induced current causes an induced electromotive force (voltage) across the ends of the conductor.
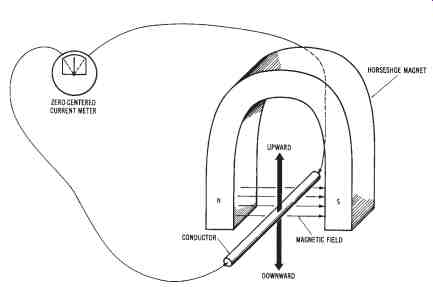
FIG. 1. Electromagnetic induction
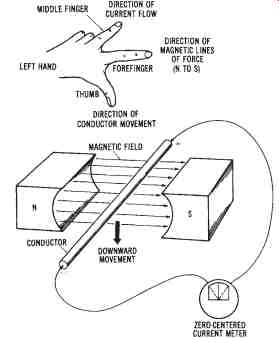
FIG. 2. Left-hand rule of induced current
BASIC GENERATOR OPERATION
As stated previously, the operation of the electrical generators used today depends upon the principle of electromagnetic induction. When conductors move through a magnetic field, or when a magnetic field is moved past conductors, an induced current develops. The current that is induced into the conductors produces an induced electromotive force or voltage.
Left-hand Rule
We can determine the direction of current flow through a moving conductor within a magnetic field by using the left-hand rule. Refer to FIG. 2 and use your left hand in the following manner:
1. Arrange your thumb, forefinger, and middle finger so that they are at approximately right angles to one another.
2. Point your thumb in the direction of conductor movement.
3. Point your forefinger in the direction of the magnetic lines of force (from north to south).
4. Your middle finger will now point in the direction of induced current flow (negative to positive).
Voltage Development in a Generator
It is known that when a conductor moves across a certain number of magnetic lines of force in one second, an induced electromotive force (emf) of one volt is developed across the conductor. Thus, the induced voltage value can be changed by modifying either the strength of the magnetic field, or the speed of conductor movement through the magnetic field. If the magnetic field is made stronger, more voltage will be induced. If the conductor is moved at a faster speed, more voltage will be induced. Likewise, if more conductors are concentrated within the magnetic field, a greater voltage will develop. These rules of electromagnetic induction are very important for the operation of mechanical generators that produce electrical power.
Sample Problem: Voltage Induced into A Conductor
In electrical generators, the coils move with respect to a magnetic field or flux. Electromagnetic induction occurs in accordance with Faraday's Law, which was formulated in 1831. This law states:
1) If a magnetic flux that links a conductor loop has relative motion, a voltage is induced, and
2) the value of the induced voltage is proportional to the rate of change of flux.
The voltage induced in a conductor of a generator is defined by Faraday's Law as follows:
Vi = B × L × v where:
Vi = induced voltage in volts,
B = magnetic flux in teslas,
L = length of conductor within the magnetic flux in meters, and
v = relative speed of the conductor in meters per second.
Given: the conductors of the stator of a generator have a length of 0.5 M. The conductors move through a magnetic field of 0.8 teslas at a rate of 68 m/s.
Find: the amount of induced voltage in each conductor.
Solution:
Vi = B × L × v
= 0.8 × 0.5 × 60
Vi = 24 Volts
SINGLE-PHASE AC POWER SYSTEMS
Electrical power can be produced by single-phase generators, commonly called alternators. The principle of operation of a single-phase alternator is shown in FIG. 3. In order for a generator to convert mechanical energy into electrical energy, three conditions must exist:
1. There must be a magnetic field developed.
2. There must be a group of conductors adjacent to the magnetic field.
3. There must be relative motion between the magnetic field and the conductors.
These conditions are necessary in order for electromagnetic induction to take place.
Generator Construction
Generators used to produce electrical power require some form of mechanical energy. This mechanical energy is used to move electrical conductors through the magnetic field of the generator. FIG. 3 shows the basic parts of a mechanical generator. A generator has a stationary part and a rotating part. The stationary part is called the stator, and the rotating part is called the rotor. The generator has magnetic field poles of north and south polarities. Also, the generator must have a method of producing a rotary motion, or a prime mover, connected to the generator shaft. There must also be a method of electrically connecting the rotating conductors to an external circuit. This is done by a slip ring/brush assembly. The stationary brushes are made of carbon and graphite. The slip rings used on AC generators are made of copper. They are permanently mounted on the shaft of the generator. The two slip rings connect to the ends of a conductor loop. When a load is connected, a closed external circuit is made. With all of these generator parts functioning together, electromagnetic induction can take place and electrical power can be produced.
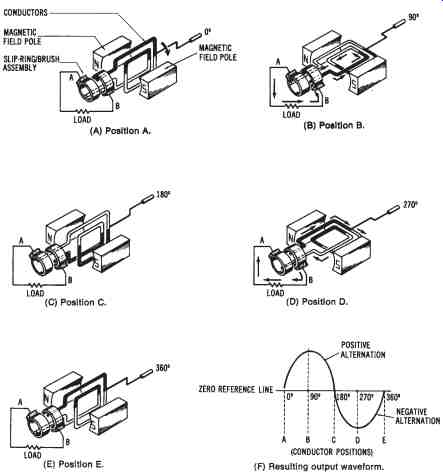
FIG. 3. Basic principle of a single-phase alternator: (A) Position A,
(B) Position B, (C) Position C, (D) Position D, (E) Position E, (F) Resulting
output waveform.
Generating AC Voltage
FIG. 3 shows a magnetic field developed by a set of permanent magnets. Conductors that can be rotated are placed within the magnetic field, and they are connected to a load device by means of a slip ring/brush assembly. FIG. 3 simulates a single-phase alternator.
In position A ( FIG. 3A), the conductors are positioned so that the minimum amount of magnetic lines of force is "cut" by the conductors as they rotate. No current is induced into the conductors at position A, and the resulting current flow through the load will be zero. If the conductors are rotated 90° in a clockwise direction to position B ( FIG. 3B), they will pass from the minimum lines of force to the most concentrated area of the magnetic field. At position B, the induced current will be maximum, as shown by the waveform diagram of FIG. 3F. Note that the induced current rises gradually from the zero reference line to a maximum value at position B. As the conductors are rotated another 90° to position C ( FIG. 3C), the induced current becomes zero again. No current flows through the load at this position. Note, in the diagram in FIG. 3F, how the induced current drops gradually from maximum to zero. This part of the induced AC (from 0° to 180°) is called the positive alternation. Each value of the induced current, as the conductors rotate from the 00 position to the 180-degree position, is in a positive direction. This action could be observed visually if a meter were connected in place of the load.
When the conductors are rotated another 90° to position D (FIG. 3D), they once again pass through the most concentrated portion of the magnetic field. Maximum current is induced into the conductors at this position. However, the direction of the induced current is in the opposite direction from that of position B. At the 270 degree position, the induced current is maximum in a negative direction. As the conductors are rotated to position E (same as at position A), the induced current is minimum once again.
Note, in the diagram of FIG. 3E, how the induced current decreases from its maximum negative value back to zero again (at the 360° position). The part of the induced current from 180° to 360° is called the negative alternation. The complete output, which shows the induced current through the load, is called an AC waveform. As the conductors continue to rotate through the magnetic field, the cycle is repeated.
AC Sine Wave
The induced current produced by the method discussed above is in the form of a sinusoidal waveform or sine wave. This waveform is referred to as a sine wave because of its mathematical origin, based on the trigonometric sine function. The current induced into the conductors, shown in FIG. 3, varies as the sine of the angle of rotation between the conductors and the magnetic field. This induced current produces a voltage. The instantaneous voltage induced into a single conductor can be expressed as:
Vi = Vmax × sin ?
where:
Vi = the instantaneous induced voltage,
Vmax = the maximum induced voltage, and
? = the angle of conductor rotation from the zero reference.
For example, at the 30° position ( FIG. 4), if the maximum voltage is 100 volts, then
Vi = 100 V × sin ?
The sine of 30° = 0.5.
Therefore:
Vi = 100 V × 0.5 = 50 volts
SINGLE-PHASE AC GENERATORS
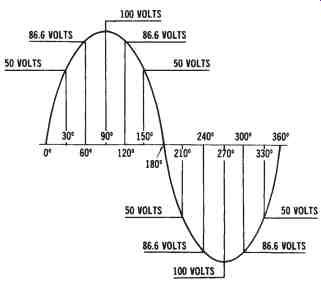
FIG. 4. Mathematic origin of an AC sine wave.
Although much single-phase electrical power is used, particularly in the home, very little electrical power is produced by single-phase alternators. The single-phase electrical power used in the home is usually developed by three-phase alternators, and then converted to single-phase electricity by the power distribution system. There are two basic methods that can be used to produce single-phase AC. One method is called the rotating-armature method, and the other is the rotating field method. These methods are illustrated in FIG. 5.
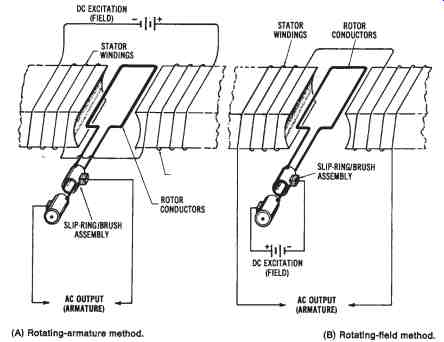
FIG. 5. The two basic methods of generating single-phase alternating cur
rent: (A) Rotating-armature method, (B) Rotating-field method
Rotating-armature Method
In the rotating-armature method, shown in FIG. 4A, an AC voltage is induced into the conductors of the rotating part of the machine. The electromagnetic field is developed by a set of stationary pole pieces. Relative motion between the conductors and the magnetic field is provided by a prime mover, or mechanical energy source, connected to the shaft (which is a part of the rotor assembly). Prime movers may be steam turbines, gas turbines, or hydraulic turbines, gasoline engines, diesel engines, or possibly gas engines, or electric motors. Remember that all generators convert mechanical energy into electrical energy, as shown in FIG. 6. Only small power ratings can be used with the rotating-armature type of alternator. The major disadvantage of this method is that the AC voltage is extracted from a slip ring/brush assembly (see FIG. 5A). A high voltage could produce tremendous sparking or arc-over between the brushes and the slip rings. The maintenance involved in replacing brushes and repairing the slip-ring commutator assembly would be very time-consuming and expensive. Therefore, this method is used only for alternators with low power ratings.
FIG. 6. Energy conversion by generators
Rotating-field Method
The rotating-field method, shown in FIG. 5B, is used for alternators capable of producing larger amounts of power. The direct current (DC) excitation voltage, which develops the magnetic field, is applied to the rotating portion of the machine. The AC voltage is induced into the stationary conductors of the machine. Since the DC-excitation voltage is a much lower value than the AC voltage that is produced, maintenance problems associated with the slip ring/brush assembly are minimized. In addition, the conductors of the stationary portion of the machine may be larger, so as to handle more current, since they do not rotate.
THREE-PHASE AC GENERATORS
The vast majority of electrical power produced in the United States is three-phase power. Because of their large power ratings, three-phase generators utilize the rotating field method. A typical three-phase generator in a power plant might have 250 volts DC excitation applied to the rotating field through the slip ring/brush assembly, while 13.8 kilovolts AC is induced into the stationary conductors.
Commercial power systems use many three-phase alternators connected in parallel to supply their regional load requirements. Normally, industrial loads represent the largest portion of the load on our power systems.
The residential (home) load is somewhat less. Because of the vast load that has to be met by the power systems, three-phase generators have high power ratings. Nameplate data for a typical commercial three-phase alternator are shown in FIG. 7. The nameplate of a generator specifies the manufacturer's rated values for the machine. It is usually a metal plate that is placed in a visible position on the generator frame. The following information would typically be listed on the nameplate:
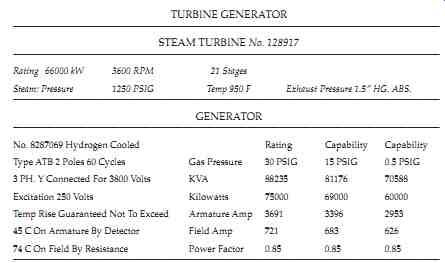
FIG. 7. Nameplate data for a commercial three-phase alternator: (A) Power
rating (in kilowatts), (B) Voltage rating (in volts), (C) Current rating
(in amperes), (D) Temperature rise (in degrees Centigrade)
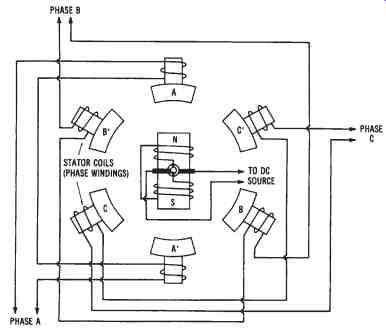
FIG. 8. Simplified drawing showing the basic construction of a three-phase
AC generator
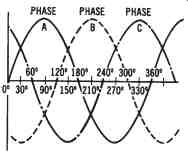
FIG. 9. Output waveforms of a three-phase AC generator
Generation of Three-phase Voltage
The basic construction of a three-phase AC generator is shown in FIG. 8, with its resulting output waveform given in FIG. 10. Note that three-phase generators must have at least six stationary poles, or two poles for each phase. The three-phase generator shown in the drawing is a rotating-field type generator. The magnetic field is developed electromagnetically by a DC voltage. The DC voltage is applied from an external power source through a slip ring/brush assembly to the windings of the rotor.
The magnetic polarities of the rotor, as shown, are north at the top and south at the bottom of the illustration. The magnetic lines of force develop around the outside of the electromagnetic rotor assembly.
Through electromagnetic induction, a current can be induced into each of the stationary (stator) coils of the generator. Since the beginning of phase A is physically located 120° from the beginning of phase B, the induced currents will be 120° apart.
Likewise, the beginnings of phase B and phase C are located 120° apart.
Thus, the voltages developed as a result of electromagnetic induction are 120° apart, as shown in FIG. 9.
Voltages are developed in each stator winding as the electromagnetic field rotates within the enclosure that houses the stator coils.
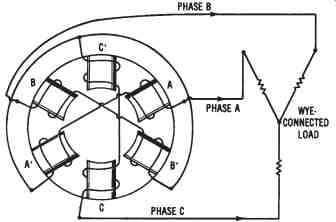
FIG. 10. Simplified drawing of the stator of a three-phase generator that
is connected in a wye configuration,
Three-Phase Connection Methods
In Figure 10, poles A', B', and C' represent the beginnings of each of the phase windings of the alternator. Poles A, B, and C represent the ends of each of the phase windings. There are two methods that may be used to connect these windings together. These methods are called wye and delta connections.
Three-phase Wye-connected Generators
The windings of a three-phase generator can be connected in a wye configuration by connecting either the beginnings or the ends of the windings together. The unconnected ends of the windings become the three phase power lines from the generator. A three-phase wye-connected generator is illustrated in FIG. 10. Notice that the beginnings of the windings (poles A', B', and C') are connected together. The other ends of the windings (poles A, B, and C) are the three-phase power lines that are connected to the load to which the generator will supply power.
Three-phase Delta-connected Generators
The windings of a three-phase generator may also be connected in a delta arrangement, as shown in FIG. 11. In the delta configuration, the beginning of one phase winding is connected to the end of the adjacent phase winding. Thus, the beginnings and ends of all adjacent phase windings are connected together. The voltage, current, and power characteristics of three-phase wye and delta connections were discussed earlier in Section 2.
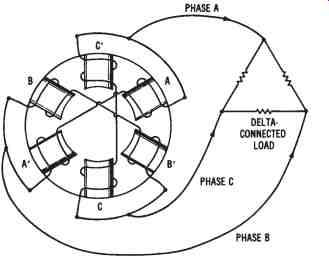
FIG. 11. Simplified drawing of the stator of a three-phase generator that
is connected in a delta configuration
Advantages of Three-phase Power
Three-phase power is used primarily for industrial and commercial applications. Many types of industrial equipment use three-phase AC power because the power produced by a three-phase voltage source, as com pared to single-phase power, is less pulsating. You can see this effect by observing that a peak voltage occurs every 120° in the three-phase wave form in FIG. 9. A single-phase voltage has a peak voltage only once every 360° ( FIG. 3). This comparison is somewhat similar to comparing the power developed by an eight-cylinder engine to the power developed by a four-cylinder engine. The eight-cylinder engine provides smoother, less-pulsating power. The effect of smoother power development on electric motors (with three-phase voltage applied) is that it produces a more uniform torque in the motor. This factor is very important for the large motors that are used in industry.
Three separate single-phase voltages can be derived from a three-phase transmission line, and three-phase power is more economical than single-phase power to distribute from plants to consumers that are located a considerable distance away. Fewer conductors are required to distribute the three-phase voltage. Also, the equipment that uses three-phase power is physically smaller in size than similar single-phase equipment.
HIGH-SPEED AND LOW-SPEED GENERATORS
Generators can also be classified as either high-speed or low-speed types ( FIG. 12). The type of generator used depends upon the prime mover used to rotate the generator. High-speed generators are usually driven by steam turbines. The high-speed generator is smaller in diameter and longer than a low-speed generator. The high-speed generator ordinarily has two stator poles per phase; thus, it will rotate at 3600 rpm to produce a 60-hertz frequency.
Low-speed generators are larger in diameter and not as long as high speed machines. Typical low-speed generators are used at hydroelectric power plants. They have large-diameter revolving fields that use many poles. The number of stator poles used could, for example, be twelve for a 600-rpm machine, or eight for a 900-rpm generator. Notice that a much larger number of poles is required for low-speed generators.
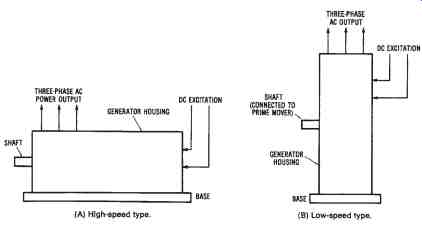
FIG. 12. High- and low-speed AC generators
GENERATOR FREQUENCY
The frequency of the sinusoidal waveforms (sine waves) produced by an AC generator is usually 60 hertz. One cycle of alternating current is generated when a conductor makes one complete revolution past a set of north and south field poles. A speed of 60 revolutions per second (3600 revolutions per minute) must be maintained to produce 60 hertz. The frequency of an AC generator (alternator) may be expressed as:
f = speed of rotation (rpm) × number of poles per phase / 120 where f is the frequency in hertz.
Sample Problem:
Given: a six-pole three-phase alternator rotates at a speed of 3600 rpm.
Find: the frequency of the alternator.
Solution:
f = N/3 × rpm / 120
6/3 × 3600 / 120 = 60 Hz
Note that if the number of poles is increased, the speed of rotation may be reduced while still maintaining a 60-Hz frequency.
HARMONICS
The voltage and current of power lines are often distorted because of the effect of harmonics. This distortion can be caused by magnetic effects in transformers, or by power control equipment. Harmonics are frequencies that are whole number multiples of the power line frequency.
Sample Problem:
Given: a power line frequency of 60 hertz is applied to an electric motor.
Find:
1. fundamental frequency
2. 3rd harmonic
3. 5th harmonic
4. 7th harmonic
Solution:
1. fundamental = 60 Hz
2. 3rd harmonic = 60 × 3 = 180 Hz
3. 5th harmonic = 60 × 5 = 300 Hz
4. 7th harmonic = 60 × 7 = 420 Hz
GENERATOR VOLTAGE REGULATION
As an increased electrical load is added to an alternator, it tends to slow down. The decreased speed causes the generated voltage to de crease. The amount of voltage change depends on the generator design and the type of load connected to its terminals. The amount of change in generated voltage from a no-load condition to a rated full-load operating condition is referred to as voltage regulation. Voltage regulation may be ex pressed as:
VR = [VNL - VFL / VFL ] × 100
where:
VR = the voltage regulation in percent,
VNL = the no-load terminal voltage, and
VFL = the rated full-load terminal voltage.
Sample Problem:
Given: a single-phase alternator has a no-load output voltage of 122.5 volts and a rated full-load voltage of 120.0 volts.
Find: the voltage regulation of the alternator.
Solution:
VR = VNL - VFL / VFL × 100
= 122.5 - 120 × 100 × 100 / 120
VR = 0.02 = 2%
GENERATOR EFFICIENCY
Generator efficiency is the ratio of the power output in watts to the power input in horsepower. The efficiency of a generator may be expressed as:
Efficiency (%) = Pout / Pin × 100
where:
Pin = the power input in horsepower, and
Pout = the power output in watts.
Sample Problem:
Given: a three-phase alternator has a power output of 22 MW and a power input of 35,000 horsepower.
Find: efficiency of the alternator.
Solution:
(%) Eff = Pout / Pin× 100
22,000,000 W/[35,000 hp × 746] × 100
%Eff = 84%
To convert horsepower to watts, remember that 1 horsepower = 746 watts.
The efficiency of a generator usually ranges from 70 percent to 85 percent.