Single-Phase Transformers

GOALS:

• discuss the different types of transformers.

• calculate values of voltage, current, and turns for single-phase transformers using formulas.

• calculate values of voltage, current, and turns for single-phase transformers using the turns ratio.

• connect a transformer and test the voltage output of different windings.

• discuss polarity markings on a schematic diagram.

• test a transformer to determine the proper polarity marks.

GLOSSARY OF SINGLE-PHASE TRANSFORMER TERMS

• autotransformer-- a transformer that uses only one winding for both the primary and secondary
• control transformer-- a common type of transformer used in motor control circuits to reduce the rated line voltage to the amount needed to operate the control components
• distribution transformer-- a transformer that is generally used to lower the power company line voltage to the value needed for houses or industrial plants
• excitation current --the amount of current that flows in the primary winding of a transformer when no load is connected to the secondary
• flux leakage-- the amount of magnetic flux lines that radiate into the air
• inrush current-- the amount of current flow that occurs when power is first applied to a transformer
• isolation transformers-- transformers that have their primary and secondary windings electrically separated from each other
• laminated-- the process of stacking thin sheets of metal together to form the core material for a transformer
• neutral conductor --a conductor is generally grounded and is a common connection to other parts of a circuit
• primary winding-- the winding of a transformer to which power is connected
• secondary winding the winding of a transformer to which the load is connected
• step-down transformer-- a transformer that produces a lower secondary voltage than primary voltage
• step-up transformer-- a transformer that produces a higher secondary voltage than primary voltage
• tape wound core --a type of transformer core made by winding a long continuous metal sheet in a circular or rounded-rectangle shape
• toroid core --a transformer core that is in a toroid shape, which is generally round with a hole in the center similar to a donut
• transformer --an electrical machine used to change values of voltage, current, and impedance
• turns ratio --the ratio of the number of turns of wire in the primary winding compared with the number of turns in the secondary winding
• volts-per-turn ratio --a method of determining voltage values in a transformer by dividing the number of turns of wire in the primary winding by the voltage applied voltage

Transformers are among the most common devices found in the electrical field. They range in size from less than one cubic inch to the size of rail cars. Their ratings can range from mVA (millivolt-amps) to GVA (giga-volt-amps). It’s imperative that anyone working in the electrical field have an understanding of transformer types and connections. This section will present transformers intended for use in single-phase installations. The two main types of voltage transformers, isolation transformers and autotransformers, will be discussed.

SINGLE-PHASE TRANSFORMERS

A transformer is a magnetically operated machine that can change values of voltage, current, and impedance without a change of frequency. Transformers are the most efficient machines known.

Their efficiencies commonly range from 90% to 99% at full load. Transformers can be divided into three classifications:

1. Isolation transformer.
2. Autotransformer.
3. Current transformer.

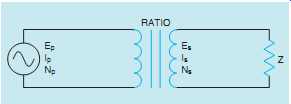
All values of a transformer are proportional to its turns ratio. This does not mean that the exact number of turns of wire on each winding must be known to determine different values of voltage and current for a transformer. What must be known is the ratio of turns. For example, assume a transformer has two windings. One winding, the primary, has 1000 turns of wire, and the other, the secondary, has 250 turns of wire (FIG. 1). The turns ratio of this transformer is 4 to 1, or 4:1 (1000/250 = 4), because there are four turns of wire on the primary for every one turn of wire on the secondary.

TRANSFORMER FORMULAS

Different formulas can be used to find the values of voltage and current for a transformer. Following is a list of standard formulas, where

NP = number of turns in the primary NS = number of turns in the secondary EP = voltage of the primary ES = voltage of the secondary IP = current in the primary IS = current in the secondary

EP ES

= NP NS EP ES

= IS IP NP NS

= IS IP or EP _ NS = ES _ NP EP _ IP = ES _ IS NP _ IP = NS _ IS

The primary winding of a transformer is the power input winding. It’s the winding that is connected to the incoming power supply. The secondary winding is the load winding, or output winding. It’s the side of the transformer that is connected to the driven load ( FIG. 2).

PRIMARY 1000 TURNS; SECONDARY 250 TURNS

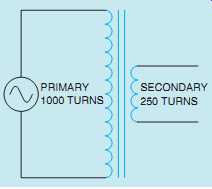
FIG. 1 All values of a transformer are proportional to its turns ratio.

LOAD SECONDARY PRIMARY

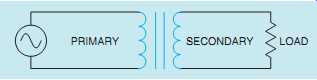
FIG. 2 An isolation transformer has its primary and secondary winding electrically separated from each other.

ISOLATION TRANSFORMERS

The transformers shown in Figures 1 and 2 are isolation transformers. This means that the secondary winding is physically and electrically isolated from the primary winding, so there is no electrical connection between the primary and secondary winding. The transformer is magnetically coupled, not electrically coupled. This line isolation is often a very desirable characteristic. Since there is no electrical connection between the load and power supply, the transformer becomes a filter between the two.

The isolation transformer will greatly reduce any voltage spikes that originate on the supply side before they are transferred to the load side. Some isolation transformers are built with a turns ratio of 1:1. A transformer of this type will have the same input and output voltage and is used for isolation only.

The isolation transformer can greatly reduce any voltage spikes before they reach the secondary because of the rise time of current through an inductor. Recall from Section 10 that the current in an inductor rises at an exponential rate (FIG. 3). As the current increases in value, the expanding magnetic field cuts through the conductors of the coil and induces a voltage that is opposed to the applied voltage. The amount of induced voltage is proportional to the rate of change of current.

This simply means that the faster the current attempts to increase, the greater the opposition to that increase will be. Spike voltages and currents are generally of very short duration, which means that they increase in value very rapidly (FIG. 4).

EXPONENTIAL CURVE TIME CURRENT SPIKE VOLTAGE SINE WAVE VOLTAGE DURATION OF VOLTAGE SPIKE

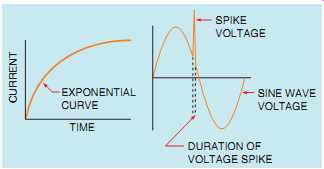
(left) FIG. 3 The current through an inductor rises at an exponential rate. (right) FIG. 4 Voltage spikes are generally of very short duration.

This rapid change of value causes the opposition to the change to increase just as rapidly. By the time the spike has been transferred to the secondary winding of the transformer, it has been eliminated or greatly reduced ( FIG. 5).

The basic construction of an isolation transformer is shown in FIG. 6. A metal core is used to provide good magnetic coupling between the two windings. The core is generally made of laminations stacked together. Laminating the core helps reduce power losses caused by eddy cur rent induction.

BASIC OPERATING PRINCIPLES

In FIG. 7, one winding of an isolation transformer has been connected to an alternating cur rent supply, and the other winding has been connected to a load. As current increases from zero to its peak positive point, a magnetic field expands outward around the coil. When the cur rent decreases from its peak positive point toward zero, the magnetic field collapses. When the current increases toward its negative peak, the magnetic field again expands, but with an opposite polarity.

The field again collapses when the current decreases from its negative peak toward zero.

This continually expanding and collapsing magnetic field cuts the windings of the primary and induces a voltage into it. This induced voltage opposes the applied voltage and limits the current flow of the primary. When a coil induces a voltage into itself, it’s known as self-induction.

EXCITATION CURRENT

There will always be some amount of current flow in the primary of any voltage transformer, regard less of type or size, even if there is no load connected to the secondary. This current flow is called the excitation current of the transformer.

The excitation current is the amount of current required to magnetize the core of the transformer.

The excitation current remains constant from no load to full load. As a general rule, the excitation current is such a small part of the full load current that it’s often omitted when making calculations.

MUTUAL INDUCTION

Since the secondary windings of an isolation transformer are wound on the same core as the primary, the magnetic field produced by the primary winding cuts the windings of the secondary also ( FIG. 8). This continually changing magnetic field induces a voltage into the secondary winding.

The ability of one coil to induce a voltage into another coil is called mutual induction. The amount of voltage induced in the secondary is determined by the ratio of the number of turns of wire in the secondary to those in the primary.

For example, assume the primary has 240 turns of wire and is connected to 120 VAC. This gives the transformer a volts-per-turn ratio of 0.5 (120 V/240 turns = 0.5 volt per turn). Now assume the secondary winding contains 100 turns of wire.

Since the transformer has a volts-per-turn ratio of 0.5, the secondary voltage will be 50 V (100 _ 0.5 = 50).

FIG. 5 The isolation transformer greatly reduces the voltage spike. PRIMARY SECONDARY LOAD

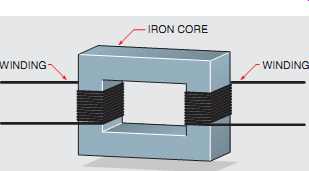
FIG. 6 Basic construction of an isolation transformer. WINDING IRON CORE WINDING

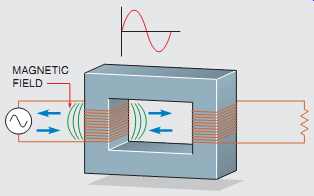
FIG. 7 Magnetic field produced by alternating current. MAGNETIC FIELD

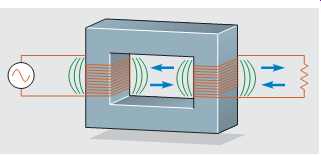
FIG. 8 The magnetic field of the primary induces a voltage into the secondary.

TRANSFORMER CALCULATIONS

In the following examples, values of voltage, cur rent, and turns for different transformers will be computed.

Assume that the isolation transformer shown in FIG. 2 has 240 turns of wire on the primary and 60 turns of wire on the secondary. This is a ratio of 4:1 (240/60 = 4). Now assume that 120 V is connected to the primary winding. What is the voltage of the secondary winding?

EP ES

= NP NS 120 ES

= 240 60 240 ES = 7200 ES = 30 V

The transformer in this example is known as a step-down transformer because it has a lower secondary voltage than primary voltage.

Now assume that the load connected to the secondary winding has an impedance of 5 ohms. The next problem is to calculate the current flow in the secondary and primary windings. The current flow of the secondary can be computed using Ohm's law since the voltage and impedance are known.

I = E Z I = 30 5 I = 6A

Now that the amount of current flow in the secondary is known, the primary current can be computed using the formula EP ES

= IS IP 120 30

= 60 IP 120 IP = 180 IP = 1:5A

Notice that the primary voltage is higher than the secondary voltage, but the primary current is much less than the secondary current. A good rule for any type of transformer is that power in must equal power out. If the primary voltage and current are multiplied together, the product should equal the product of the voltage and current of the secondary.

Primary Secondary 120 _ 1:5 = 180 VA 30 _ 6 = 180 VA

In this example, assume that the primary winding contains 240 turns of wire and the secondary contains 1200 turns of wire. This is a turns ratio of 1:5 (1200/240 = 5). Now assume that 120 V is connected to the primary winding. Compute the voltage output of the secondary winding.

EP ES

= NP NS 120 ES

= 240 1200 240 ES = 144,000 ES = 600 V

Notice that the secondary voltage of this transformer is higher than the primary voltage. This is known as a step-up transformer.

Now assume that the load connected to the secondary has an impedance of 2400 O. Find the amount of current flow in the primary and secondary windings. The current flow in the secondary winding can be computed using Ohm's law.

I = E Z I = 600 2400 I = 0:25 A

Now that the amount of current flow in the secondary is known, the primary current can be computed using the formula EP ES

= IS IP 120 600 = 0:25 IP 120 IP = 150 IP = 1:25 A

Notice that the amount of power input equals the amount of power output.

Primary Secondary

120 _ 1:25 = 150 VA 600 _ 0:25 = 150 VA

CALCULATING ISOLATION TRANSFORMER VALUES USING THE TURNS RATIO

As illustrated in the previous examples, transformer values of voltage, current, and turns can be computed using formulas. It’s also possible to compute these values using the turns ratio. To make calculations using the turns ratio, a ratio is established that compares some number to 1, or 1 to some number. For example, assume a transformer has a primary rated at 240 V and a secondary rated at 96 V ( FIG. 9). The turns ratio can be computed by dividing the higher voltage by the lower voltage.

Ratio = 240 96

Ratio = 2:5:1

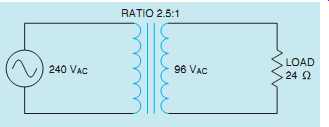
FIG. 9 Computing transformer values using the turns ratio.

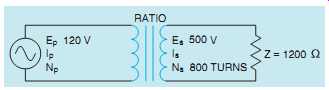
FIG. 10 Calculating transformer values.

This ratio indicates that there are 2.5 turns of wire in the primary winding for every 1 turn of wire in the secondary. The side of the transformer with the lowest voltage will always have the lowest number (1) of the ratio.

Now assume that a resistance of 24 ohm is connected to the secondary winding. The amount of secondary current can be found using Ohm's law.

IS = 96 24 IS = 4A

The primary current can be found using the turns ratio. Recall that the volt-amps of the primary must equal the volt-amps of the secondary.

Since the primary voltage is greater, the primary current will have to be less than the secondary current.

IP = IS turns ratio IP = 4 2:5 IP = 1:6A

To check the answer, find the volt-amps of the primary and secondary.

Primary Secondary 240 _ 1:6 = 384 VA 96 _ 4 = 384 VA

Now assume that the secondary winding contains 150 turns of wire. The primary turns can be found by using the turns ratio also. Since the primary voltage is higher than the secondary voltage, the primary must have more turns of wire.

NP = NS _ turns ratio NP = 150 _ 2:5 NP = 375 turns

In the next example, assume an isolation transformer has a primary voltage of 120 V and a secondary voltage of 500 V. The secondary has a load impedance of 1200 Ohm. The secondary contains 800 turns of wire ( FIG. 10).

The turns ratio can be found by dividing the higher voltage by the lower voltage.

Ratio = 500 120 Ratio = 1:4:17

The secondary current can be found using Ohm's law.

IS = 500 1200 IS = 0:417 A

In this example, the primary voltage is lower than the secondary voltage. Therefore, the primary current must be higher.

IP = IS _ turns ratio IP = 0:417 _ 4:17 IP = 1:74A

To check this answer, compute the volt-amps of both windings.

Primary Secondary

120_1:74 = 208:8 VA 500_0:417 = 208:5VA

The slight difference in answers is caused by rounding off values.

Since the primary voltage is less than the secondary voltage, the turns of wire in the primary will be less also.

NP = NS turns ratio NP = 800 4:17 NP = 192 turns FIG. 11 shows the transformer with all completed values.

FIG. 11 Transformer with completed values.

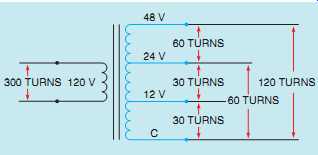
FIG. 13 Transformer secondary with multiple taps.

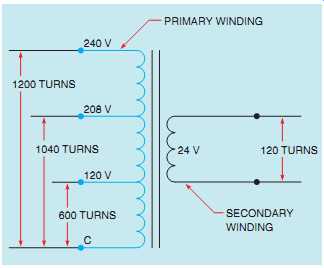
FIG. 12 Transformer with multiple-tapped primary winding.

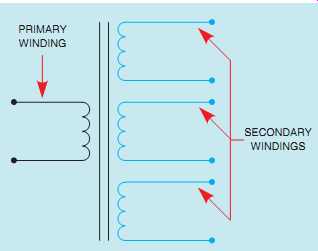
FIG. 14 Transformer with multiple secondary windings.

MULTIPLE-TAPPED WINDINGS

It’s not uncommon for isolation transformers to be designed with windings that have more than one set of lead wires connected to the primary or secondary.

These are called multiple-tapped windings. The transformer shown in FIG. 12 contains a secondary winding rated at 24 V. The primary winding contains several taps, however. One of the primary lead wires is labeled C and is the common for the other leads.

The other leads are labeled 120, 208, and 240. This transformer is designed so that it can be connected to different primary voltages without changing the value of the secondary voltage. In this example, it’s assumed that the secondary winding has a total of 120 turns of wire. To maintain the proper turns ratio, the primary would have 600 turns of wire between C and 120,1040 turns between C and 208, and 1200 turns between C and 240.

The isolation transformer shown in FIG. 13 contains a single primary winding. The secondary winding, however, has been tapped at several points. One of the secondary lead wires is labeled C and is common to the other lead wires. When rated voltage is applied to the primary, voltages of 12, 24, and 48 V can be obtained at the secondary. It should be noted also that this arrangement of taps permits the transformer to be used as a center-tapped transformer for two of the voltages.

If a load is placed across the lead wires labeled C and 24, the lead wire labeled 12 becomes a center tap. If a load is placed across the C and 48 lead wires, the 24 lead wire becomes a center tap.

In this example, it’s assumed that the primary winding has 300 turns of wire. To produce the proper turns ratio would require 30 turns of wire between C and 12, 60 turns of wire between C and 24, and 120 turns of wire between C and 48.

The isolation transformer shown in FIG. 14 is similar to the transformer in FIG. 13. The one in FIG. 14, however, has multiple secondary windings instead of a single secondary winding with multiple taps. The advantage is that the secondary windings are electrically isolated from each other. These secondary windings can be either step up or step-down depending on the application of the transformer.

COMPUTING VALUES FOR ISOLATION TRANSFORMERS WITH MULTIPLE SECONDARIES

When computing the values of an isolation transformer with multiple secondary windings, each secondary must be treated as a different transformer.

For example, the transformer in FIG. 15 contains one primary winding and three secondary windings. The primary is connected to 120 VAC and has 300 turns of wire. One secondary has an output voltage of 560 V and a load impedance of 1000 Ohm. The second secondary has an output volt age of 208 V and a load impedance of 400 Ohm, and the third secondary has an output voltage of 24 V and a load impedance of 6 Ohm. The current, turns of wire, and ratio for each secondary, and the current of the primary will be found.

The first step will be to compute the turns ratio of the first secondary. This can be done by dividing the smaller voltage into the larger.

Ratio = ES1 EP Ratio = 560 120 Ratio = 1:4:67

The current flow in the first secondary can be computed using Ohm's law.

IS1 = 560 1000 IS1 = 0:56 A The number of turns of wire in the first secondary winding will be found using the turns ratio.

Since this secondary has a higher voltage than the primary, it must have more turns of wire.

NS1 = NP / turns ratio

NS1 = 300 _ 4:67

NS1 = 1401 turns

The amount of primary current needed to supply this secondary winding can be found using the turns ratio also. Since the primary has less voltage, it will require more current.

IP (FIRST SECONDARY ) = IS1 _ turns ratio IP (FIRST SECONDARY ) = 0:56 _ 4:67 IP (FIRST SECONDARY ) = 2:61 A

The turns ratio of the second secondary winding will be found by dividing the higher voltage by the lower.

Ratio = 208 120 Ratio = 1:1:73

The amount of current flow in this secondary can be determined using Ohm's law.

IS2 = 208 400 IS2 = 0:52 A

Since the voltage of this secondary is greater than the primary, it will have more turns of wire than the primary. The turns of this secondary will be found using the turns ratio.

NS2 = NP _ turns ratio NS2 = 300 _ 1:73 NS2 = 519 turns

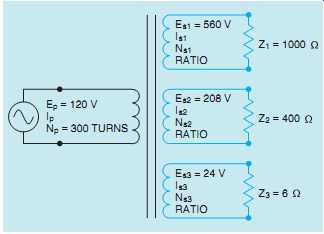
FIG. 15 Computing values for a transformer with multiple secondary windings.

The voltage of the primary is less than this secondary. The primary will, therefore, require a greater amount of current. The amount of current required to operate this secondary will be computed using the turns ratio.

IP (SECOND SECONDARY ) = IS2 _ turns ratio IP (SECOND SECONDARY ) = 0:52 _ 1:732 IP (SECOND SECONDARY ) = 0:9A

The turns ratio of the third secondary winding will be computed in the same way as the other two.

The larger voltage will be divided by the smaller.

Ratio = 120 24 Ratio = 5:1 The primary current will be found using Ohm's law.

IS3 = 24 6 IS3 = 4A

The output voltage of the third secondary is less than the primary. The number of turns of wire will, therefore, be less than the primary turns.

NS3 = NP turns ratio NS3 = 300 5 NS3 = 60 turns

The primary has a higher voltage than this secondary. The primary current will, therefore, be less by the amount of the turns ratio.

IP (THIRD SECONDARY ) = IS3/turns ratio

IP (THIRD SECONDARY ) = 4/5

IP (THIRD SECONDARY ) = 0:8A

The primary must supply current to each of the three secondary windings. Therefore, the total amount of primary current will be the sum of the currents required to supply each secondary.

IP (TOTAL ) = IP1 ) IP2 ) IP3 IP (TOTAL ) = 2:61 ) 0:9 ) 0:8 IP (TOTAL ) = 4:31 A

The transformer with all computed values is shown in FIG. 16.

CH

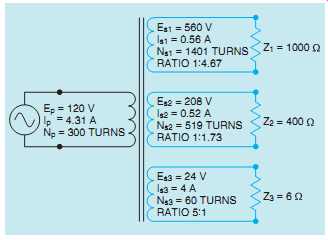
FIG. 16 The transformer with all computed values.

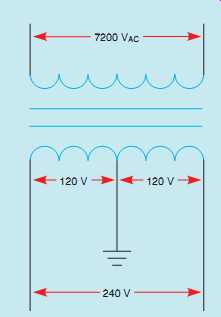
FIG. 17 Distribution transformer.

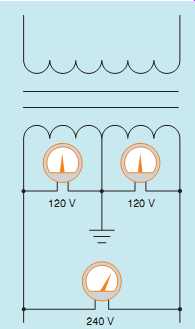
FIG. 18 The voltage from either line to neutral is 120 V. The voltage across the entire secondary winding is 240 V.

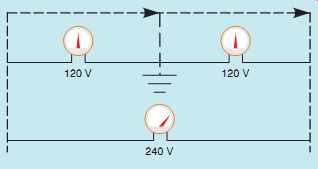
FIG. 19 The voltages across the secondary are in phase with each other.

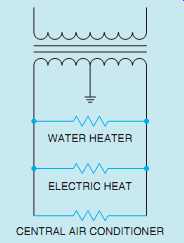
FIG. 20 240-V loads connect directly across the secondary winding.

DISTRIBUTION TRANSFORMERS

A common type of isolation transformer is the distribution transformer, FIG. 17. This transformer changes the high voltage of power company distribution lines to the common 240/120 V that supplies power to most homes and many businesses. In this example, it’s assumed that the primary is connected to a 7200-V line. The secondary is 240 V with a center tap. The center tap is grounded and becomes the neutral conductor or common conductor. If voltage is measured across the entire secondary, a voltage of 240 V will be seen. If voltage is measured from either line to the center tap, half of the secondary voltage, or 120 V, will be seen ( FIG. 18). This occurs because the grounded neutral conductor becomes the center point of two in-phase voltages. A vector diagram drawn to illustrate this condition, shows that the grounded neutral conductor is connected to the center point of the two in-phase voltages ( FIG. 19). Loads that are intended to operate on 240 V, such as water heaters, electric resistance heating units, and central air conditioners are connected directly across the lines of the secondary (FIG. 20).

Loads that are intended to operate on 120 V connect from the center tap, or neutral, to one of the secondary lines. The function of the neutral is to carry the difference in current between the two secondary lines and maintain a balanced voltage.

In FIG. 21, one of the secondary lines has a current flow of 30 A and the other has a current flow of 24 A. The neutral conducts the sum of the unbalanced load. In this example, the neutral current will be 6 A (30 _ 24 = 6).

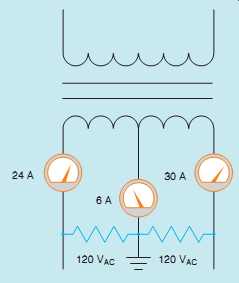
FIG. 21 The neutral carries the sum of the unbalanced load.

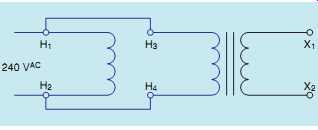
FIG. 23 Control transformer connected for 240-V operation.

FIG. 22 Control transformer with fuse protection added to the secondary winding.

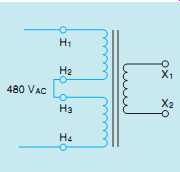
FIG. 24 Control transformer connected for 480-V operation.

CONTROL TRANSFORMERS

Another common type of isolation transformer found throughout industry is the control transformer ( FIG. 22). The control transformer reduces line voltage to the value needed to operate control circuits. The most common type of control transformer contains two primary windings and one secondary. The primary windings are generally rated at 240 V each, and the secondary at 120 V.

This arrangement provides a 2:1 turns ratio between each of the primary windings and the secondary. For example, assume that each of the primary windings contains 200 turns of wire. The secondary will contain 100 turns of wire.

One of the primary windings in FIG. 23 is labeled H1 and H2. The other is labeled H3 and H4.

The secondary winding is labeled X1 and X2. If the primary of the transformer is to be connected to 240 V, the two primary windings will be connected in parallel by connecting H1 and H3 together, and H2 and H4 together. When the primary windings are connected in parallel, the same voltage is applied across both windings. This has the same effect as using one primary winding with a total of 200 turns of wire. A turns ratio of 2:1 is maintained, and the secondary voltage is 120 V.

If the transformer is to be connected to 480 V, the two primary windings will be connected in series by connecting H2 and H3 together ( FIG. 24). The incoming power is connected to H1 and H4.

Series-connecting the primary windings increases the number of turns in the primary to 400. This produces a turns ratio of 4:1. When 480 V is connected to the primary, the secondary voltage remains at 120.

The primary leads of a control transformer are generally cross-connected, as shown in FIG. 25, so metal links can be used to connect the primary for 240- or 480-V operation. If the primary is to be connected for 240-V operation, the metal links are connected under screws as shown in FIG. 26.

Notice that leads H1 and H3 are connected together and leads H2 and H4 are connected together.

Compare this connection with the connection shown in FIG. 23.

If the transformer is to be connected for 480-V operation, terminals H2 and H3 are connected as shown in FIG. 27. Compare this connection with the connection shown in FIG. 24.

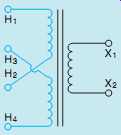
FIG. 25 The primary windings of a control transformer are crossed.

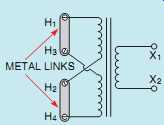
FIG. 26 Metal links connect transformer for 240-V operation.

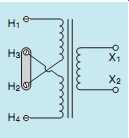
FIG. 27 Control transformer connected for 480-V operation.

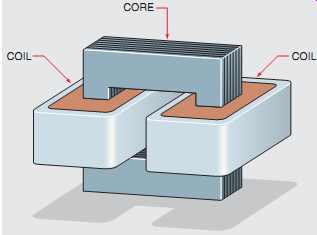
FIG. 28 Core of a 600-MVA three-phase
transformer. At Houston Lighting and Power.

FIG. 29 A core type transformer.

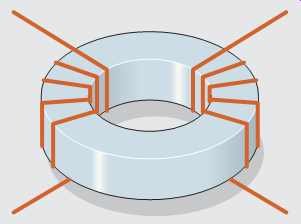
FIG. 32 A toroid transformer.

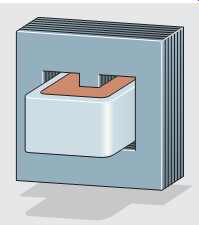
FIG. 30 A shell type transformer.

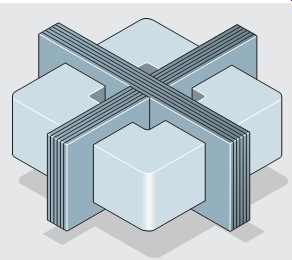
FIG. 31 A transformer with an H type core.

TRANSFORMER CORE TYPES

Several types of cores are used in the construction of transformers. Most cores are made from thin steel punchings laminated together to form a solid metal core. The core for a 600-MVA (mega-volt-amp) three-phase transformer is shown in FIG. 28. Laminated cores are preferred because a thin layer of oxide forms on the surface of each lamination and acts as an insulator to reduce the formation of eddy currents inside the core material. The amount of core material needed for a particular transformer is determined by the power rating of the transformer, but it must be sufficient to prevent saturation at full load.

The type and shape of the core generally determine the amount of magnetic coupling between the windings and to some extent the efficiency of the transformer.

The transformer illustrated in FIG. 29 is known as a core type transformer. The windings are placed around each end of the core material.

The shell type transformer is constructed in a similar manner to the core type, except that the shell type has a metal core piece through the middle of the window ( FIG. 30). The primary and secondary windings are wound around the center core piece with the low-voltage winding being closest to the metal core. This arrangement permits the transformer to be surrounded by the core and provides excellent magnetic coupling. When the transformer is in operation, all the magnetic flux must pass through the center core piece. It then divides through the two outer core pieces.

The H type core shown in FIG. 31 is similar to the shell type core in that it has an iron core through its center around which the primary and secondary windings are wound. The H core, how ever, surrounds the windings on four sides instead of two. This extra metal helps reduce stray leakage flux and improve the efficiency of the transformer.

The H type core is often found on high-voltage distribution transformers.

The tape wound core or toroid core ( FIG. 32) is constructed by tightly winding one long continuous silicon steel tape into a spiral. The tape may or may not be housed in a plastic container, depending on the application. This type of core does not require steel punchings laminated together. Since the core is one continuous length of metal, flux leakage is kept to a minimum. Flux leakage is the magnetic flux lines that don’t follow the metal core and are lost to the surrounding air. The tape wound core is one of the most efficient core designs available.

FIG. 32

TRANSFORMER INRUSH CURRENT

A reactor is an inductor used to add inductance to the circuit. Although transformers and reactors are both inductive devices, there is a great difference in their operating characteristics. Reactors are often connected in series with a low-impedance load to prevent inrush current (the amount of current that flows when power is initially applied to the circuit) from becoming excessive ( FIG. 33). Transformers, however, can produce extremely high inrush currents when power is first applied to the primary winding. The type of core used when constructing inductors and transformers is primarily responsible for this difference in characteristics.

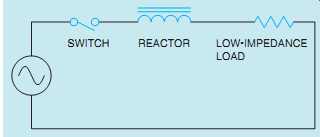
FIG. 33 Reactors help prevent inrush current from becoming excessive when power is first turned on.

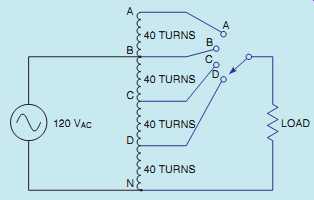
FIG. 34 An autotransformer has only one winding, which is used for both the primary and secondary.

AUTOTRANSFORMERS

Autotransformers are one-winding transformers.

They use the same winding for both the primary and secondary. The primary winding in FIG. 34 is between points B and N and has a voltage of 120 V applied to it. Between points B and N, there are 120 turns of wire. Now assume that the selector switch is set to point D. The load is now connected between points D and N. The secondary of this transformer contains 40 turns of wire. If the amount of voltage applied to the load is to be computed, the following formula can be used.

EP ES

= NP NS 120 ES

= 120 40 120 ES = 4800 ES = 40 V

Assume that the load connected to the secondary has an impedance of 10 Ohm. The amount of cur rent flow in the secondary circuit can be computed using the formula

I = E Z I = 40 10 I = 4A

The primary current can be computed using the same formula that was used to compute primary current for an isolation type of transformer.

EP ES

= IS IP 120 40

= 4 IP 120 IP = 160 IP = 1:333 A

The amount of power input and output for the autotransformer must be the same, just as they are in an isolation transformer.

Primary Secondary

120 _ 1:333 = 160 VA 40 _ 4 = 160 VA Now assume that the rotary switch is connected to point A. The load is now connected to 160 turns of wire. The voltage applied to the load can be computed by

EP ES

= NP NS 120 ES

= 120 160 120 ES = 19,200 ES = 160 V

===

SHAFT BRUSH HOLDER CARBON BRUSH POWERKOTE COIL CORE BASE SHAFT BEARINGS END FORMS RADIATOR GOLD PLATED COMMUTATOR TERMINAL BOARD

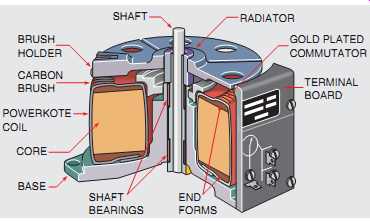
FIG. 35 Cutaway view of a powerstat.

===

Notice that the autotransformer, like the isolation transformer, can be either a step-up or step down transformer.

If the rotary switch shown in FIG. 34 were removed and replaced with a sliding tap that made contact directly to the transformer winding, the turns ratio could be adjusted continuously.

This type of transformer is commonly referred to as a Variac or Powerstat, depending on the manufacturer. A cutaway view of a variable autotransformer is shown in FIG. 35. The windings are wrapped around a tape-wound toroid core inside a plastic case. The tops of the windings have been milled flat to provide a commutator. A carbon brush makes contact with the windings.

Autotransformers are often used by power companies to provide a small increase or decrease to line voltage. They help provide voltage regulation to large power lines. A three-phase autotransformer is shown in FIG. 36. This transformer is contained in a housing filled with transformer oil, which acts as a coolant and prevents moisture from forming in the windings.

The autotransformer does have one disadvantage. Since the load is connected to one side of the power line, there is no line isolation between the incoming power and the load. This can cause problems with certain types of equipment and must be a consideration when designing a power system.

TRANSFORMER POLARITIES

To understand transformer polarity, the voltage produced across a winding must be considered during some point in time. In a 60-Hz AC circuit, the voltage changes polarity 60 times per second. When discussing transformer polarity, it’s necessary to consider the relationship between the different windings at the same point in time. It will, therefore, be assumed that this point in time is when the peak positive voltage is being produced across the winding.

FIG. 36 Three-phase autotransformer.

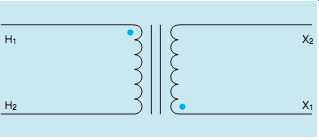
FIG. 37 Transformer polarity dots.

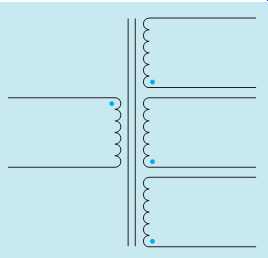
FIG. 38 Polarity marks for multiple secondaries.

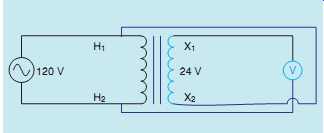
FIG. 39 Connecting the secondary and primary windings forms an autotransformer.

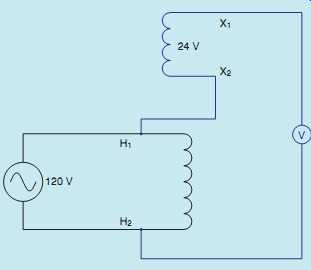
FIG. 40 Redrawing the connection.

POLARITY MARKINGS ON SCHEMATICS

When a transformer is shown on a schematic diagram it’s common practice to indicate the polarity of the transformer windings by placing a dot beside one end of each winding, as shown in FIG. 37.

These dots signify that the polarity is the same at that point in time for each winding. For example, assume the voltage applied to the primary winding is at its peak positive value at the terminal indicated by the dot. The voltage at the dotted lead of the secondary will be at its peak positive value at the same time.

This same type of polarity notation is used for transformers that have more than one primary or secondary winding. An example of a transformer with a multisecondary is shown in FIG. 38.

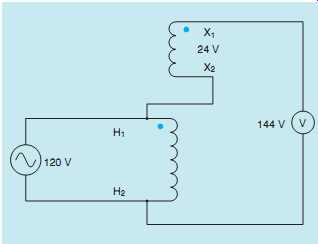
FIG. 41 Placing polarity dots to indicate additive polarity.

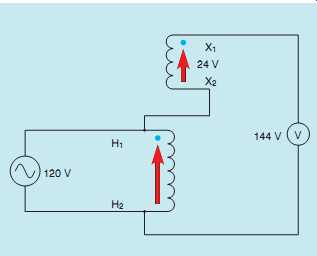
FIG. 43 Arrows help indicate the placement of the polarity dots.

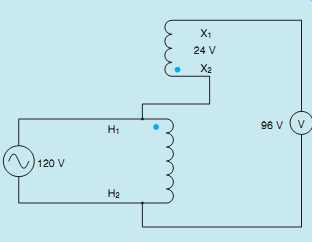
FIG. 42 Polarity dots indicate subtractive polarity.

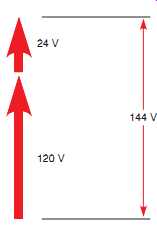
FIG. 44 The values of the arrows add to indicate additive polarity (boost connection).

ADDITIVE AND SUBTRACTIVE POLARITIES

The polarity of transformer windings can be deter mined by connecting them as an autotransformer and testing for additive or subtractive polarity, often referred to as a boost or buck connection.

This is done by connecting one lead of the secondary to one lead of the primary and measuring the voltage across both windings ( FIG. 39). The transformer shown in the example has a primary voltage rating of 120 V and a secondary voltage rating of 24 V. This same circuit has been redrawn in FIG. 40 to show the connection more clearly. Notice that the secondary winding has been connected in series with the primary winding.

The transformer now contains only one winding and is, therefore, an autotransformer. When 120 V is applied to the primary winding, the volt meter connected across the secondary will indicate either the sum of the two voltages or the difference between the two voltages. If this voltmeter indicates 144 V (120 ) 24 = 144) the windings are connected additive (boost), and polarity dots can be placed as shown in FIG. 41. Notice in this connection that the secondary voltage is added to the primary voltage.

If the voltmeter connected to the secondary winding indicates a voltage of 96 V (120 _ 24 = 96) the windings are connected subtractive (buck), and polarity dots are placed as shown in FIG. 42.

USING ARROWS TO PLACE DOTS

To help in the understanding of additive and subtractive polarity, arrows can be used to indicate a direction of greater than or less than values. In FIG. 43, arrows have been added to indicate the direction in which the dot is to be placed.

In this example, the transformer is connected additive, or boost, and both of the arrows point in the same direction. Notice that the arrow points to the dot. In FIG. 44, it’s seen that values of the two arrows add to produce 144 V.

In FIG. 45, arrows have been added to a subtractive, or buck, connection. In this instance, the arrows point in opposite directions, and the voltage of one tries to cancel the voltage of the other. The result is that the smaller value is eliminated, and the larger value is reduced as shown in FIG. 46.

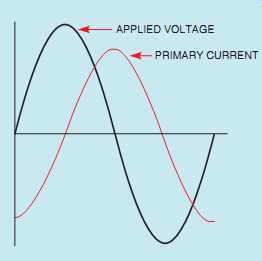
FIG. 47 At no load, the primary current lags the voltage by 90°.

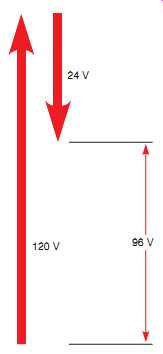
FIG. 46 The arrows help indicate subtractive polarity.

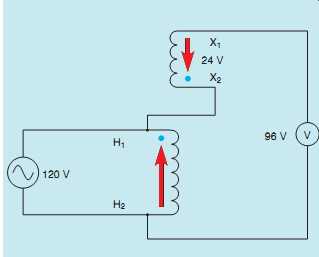
FIG. 45 The values of the arrows subtract (buck connection).

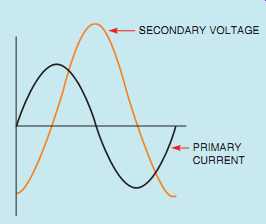
FIG. 48 The secondary voltage lags the primary current by 90°.

VOLTAGE AND CURRENT RELATIONSHIPS IN A TRANSFORMER

When the primary of a transformer is connected to power but there is no load connected to the secondary, current is limited by the inductive reactance of the primary. At this time, the transformer is essentially an inductor, and the excitation current is lagging the applied voltage by 90° ( FIG. 47). The primary current induces a voltage in the secondary.

This induced voltage is proportional to the rate of change of current. The secondary voltage will be maximum during the periods when the primary current is changing the most (0°, 180°, and 360°), and it will be zero when the primary current is not changing (90° and 270°). A plot of the primary current and secondary voltage shows that the secondary voltage lags the primary current by 90° ( FIG. 48). Because the secondary voltage lags the primary current by 90° and the applied voltage leads the primary current by 90°, the secondary voltage is 180° out of phase with the applied voltage and in phase with the induced voltage in the primary.

ADDING LOAD TO THE SECONDARY

When a load is connected to the secondary, current begins to flow. Because the transformer is an inductive device, the secondary current lags the secondary voltage by 90°. Since the secondary volt age lags the primary current by 90°, the secondary current is 180° out of phase with the primary current ( FIG. 49).

The current of the secondary induces a counter voltage in the secondary windings that is in opposition to the counter-voltage induced in the primary.

The counter-voltage of the secondary weakens that of the primary and permits more primary current to flow. As secondary current increases, primary current increases proportionally.

Since the secondary current causes a decrease in the counter-voltage produced in the primary, the cur rent of the primary is limited less by inductive reactance and more by the resistance of the windings as load is added to the secondary. A wattmeter connected to the primary would show that the true power increases as load is added to the secondary.

===

APPLIED VOLTAGE SECONDARY CURRENT PRIMARY CURRENT SECONDARY VOLTAGE

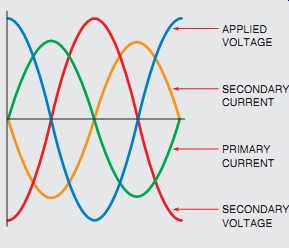
FIG. 49 Voltage and current relationships of the primary and secondary windings.

===

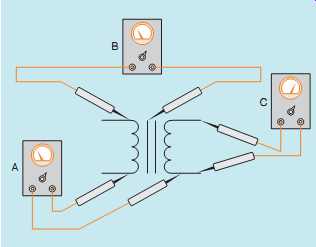
FIG. 50 Testing a transformer with an ohmmeter.

===

TESTING THE TRANSFORMER

Several tests can be made to determine the condition of the transformer. A simple test for grounds, shorts, or opens can be made with an ohmmeter ( FIG. 50). Ohmmeter A is connected to one lead of the primary and one lead of the secondary.

This test checks for shorted windings between the primary and secondary. The ohmmeter should indicate infinity. If there is more than one primary or secondary winding, all isolated windings should be tested for shorts. Ohmmeter B illustrates testing the windings for grounds. One lead of the ohmmeter is connected to the case of the transformer, and the other is connected to the winding. All windings should be tested for grounds, and the ohmmeter should indicate infinity for each winding. Ohmmeter C illustrates testing the windings for continuity. The wire resistance of the winding should be indicated by the ohmmeter.

If the transformer appears to be in good condition after the ohmmeter test, it should then be tested for shorts and grounds with a megohmmeter. A MEGGER will reveal problems of insulation break down that an ohmmeter will not. The condition of the dielectric oil in large oil-filled transformers should be tested at periodic intervals. This involves taking a sample of the oil and performing tests for dielectric strength and contamination.

TRANSFORMER RATINGS

Most transformers have a nameplate with information concerning the transformer. The information listed is generally determined by the size, type, and manufacturer. Almost all nameplates list the primary voltage, secondary voltage, and KVA (kilo-volt-amps) rating. Transformers are rated in kilo-volt-amps and not kilowatts because the true power is determined by the power factor of the load. Other information that may or may not be listed is frequency, temperature rise in C°, impedance, type of insulating oil, gallons of insulating oil, serial number, type number, model number, and whether the transformer is single-phase or three-phase.

DETERMINING MAXIMUM CURRENT

The nameplate does not list the current rating of the windings. Since power input must equal power out put, the current rating for a winding can be deter mined by dividing the kVA rating by the winding voltage. For example, assume a transformer has a kVA rating of 0.5 kVA, a primary voltage of 480 V, and a secondary voltage of 120 V. To determine the maximum current that can be supplied by the secondary, divide the KVA rating by the secondary voltage.

IS = kVA ES IS = 500 120 IS = 4:16 A

The primary current can be computed in the same way.

IP = kVA EP IP = 500 480 IP = 1:04 A

Transformers with multiple secondary windings generally have the current rating listed with the voltage rating.

++++++++++

EXAMPLE 1

Assume that the transformer shown in FIG. 51 is a 2400/480 volt 15 kVA transformer. To determine the impedance of the transformer, first compute the full-load current rating of the secondary winding.

I5 VA E I5 15,000 480 I531:25 A

Next, increase the source voltage connected to the high-voltage winding until a current of 31.25 amperes flows in the low voltage winding. Assume that the voltage value is 138 volts. Finally, determine the percentage of applied voltage compared with the rated voltage.

%Z5 source voltage rated voltage 3100

%Z5 138 2400 3100

%Z50:05753100

%Z55:75 The impedance of this transformer is 5.75%.

Transformer impedance is a major factor in determining the amount of voltage drop a transformer will exhibit between no load and full load and in determining the amount of current flow in a short-circuit condition. Short-circuit current can be computed using the formula (Single phase) ISC 5 VA E3%Z The formula for determining current in a single-phase circuit is I5 VA E The preceding formula for determining short-circuit current can be modified to show that the short-circuit current can be computed by dividing the rated secondary current by the %Z.

ISC 5 I Rated %Z

++++++++++

EXAMPLE 2

A single-phase transformer is rated at 50 kVA and has a secondary voltage of 240 volts. The nameplate reveals that the transformer has an internal impedance (%IZ) of 2.5%. What is the short-circuit current for this transformer? I Secondary 5 50,000 240 I Secondary 5208:3 amperes I Short circuit 5 208:3

%Z I Short circuit 5 208:3

0:025 I Short circuit 58,333:3 amperes It’s sometimes necessary to compute the amount of short-circuit current when determining the correct fuse rating for a circuit. The fuse must have a high enough "interrupt" rating to clear the fault in the event of a short circuit.

++++++++++

===

VARIABLE VOLTAGE SOURCE VOLTMETER HIGH-VOLTAGE WINDING LOW-VOLTAGE WINDING AMMETER SHORT CIRCUIT

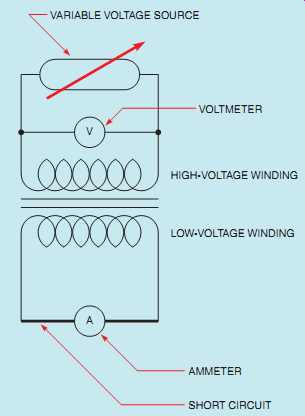
FIG. 51 Determining transformer impedance.

===

TRANSFORMER IMPEDANCE

Transformer impedance is determined by the physical construction of the transformer. Factors such as the amount and type of core material, wire size used to construct the windings, number of turns, and degree of magnetic coupling between the windings greatly affect the transformer's impedance.

Impedance is expressed as a percent (%Z or %IZ) and is measured by connecting a short circuit across the low-voltage winding of the transformer and then connecting a variable voltage source to the high-voltage winding, FIG. 51. The variable voltage is then increased until rated cur rent flows in the low-voltage winding. The transformer impedance is determined by calculating the percentage of variable voltage compared with the rated voltage of the high-voltage winding.

SUMMARY

• All values of voltage, current, and impedance in a transformer are proportional to the turns ratio.

• Transformers can change values of voltage, current, and impedance, but cannot change the frequency.

• The primary winding of a transformer is connected to the power line.

• The secondary winding is connected to the load.

• A transformer that has a lower secondary voltage than primary voltage is a step-down transformer.

• A transformer that has a higher secondary voltage than primary voltage is a step-up transformer.

• An isolation transformer has its primary and secondary windings electrically and mechanically separated from each other.

• When a coil induces a voltage into itself, it’s known as self-induction.

• When a coil induces a voltage into another coil, it’s known as mutual induction.

• Transformers can have very high inrush current when first connected to the power line because of the magnetic domains in the core material.

• Inductors provide an air gap in their core material that causes the magnetic domains to reset to a neutral position.

• Autotransformers have only one winding, which is used as both the primary and secondary.

• Autotransformers have a disadvantage in that they have no line isolation between the primary and secondary winding.

• Isolation transformers help filter voltage and current spikes between the primary and secondary side.

• Polarity dots are often added to schematic diagrams to indicate transformer polarity.

• Transformers can be connected as additive or subtractive polarity.

QUIZ:

1. What is a transformer?

2. What are common efficiencies for transformers?

3. What is an isolation transformer?

4. All values of a transformer are proportional to its .

5. What is an autotransformer?

6. What is a disadvantage of an autotransformer?

7. Explain the difference between a step-up and a step-down transformer.

8. A transformer has a primary voltage of 240 V and a secondary voltage of 48 V. What is the turns ratio of this transformer?

9. A transformer has an output of 750 VA. The primary voltage is 120 V. What is the primary current?

10. A transformer has a turns ratio of 1:6. The primary current is 18 A. What is the secondary current?

11. What do the dots shown beside the terminal leads of a transformer represent on a schematic? 12. A transformer has a primary voltage rating of 240 V and a secondary voltage rating of 80 V. If the windings were connected subtractive, what voltage would appear across the entire connection?

12 were to be connected additive, what voltage would appear across the entire winding?

13. If the windings of the transformer in question

14. The primary leads of a transformer are labeled 1 and 2. The secondary leads are labeled 3 and 4. If polarity dots are placed beside leads 1 and 4, which secondary lead would be connected to terminal 2 to make the connection additive?

PRACTICE PROBLEMS

Refer to FIG. 52 to answer the following questions. Find all the missing values.

1.

EP 120 ES 24 IP IS NP 300 NS Ratio Z = 3 Ohm 2.

EP 240 ES 320 IP IS NP NS 280 Ratio Z = 500 Ohm 3.

EP ES 160 IP IS NP NS 80 Ratio 1:2.5 Z = 12 Ohm 4.

EP 48 ES 240 IP IS NP 220 NS Ratio Z = 360 Ohm 5.

EP ES IP 16.5 IS 3.25 NP NS 450 Ratio Z = 56 Ohm 6.

EP 480 ES IP IS NP 275 NS 525 Ratio Z = 1.2 k-Ohm.

Refer to FIG. 53 to answer the following questions. Find all the missing values.

7.

EP 208 ES1 320 ES2 120 ES3 24 IP IS1 IS2 IS3 NP 800 NS1 NS2 NS3 Ratio 1: Ratio 2: Ratio 3:

R1 12 k-Ohm, R2 6 O R3 8 O 8.

EP 277 ES1 480 ES2 208 ES3 120 IP IS1 IS2 IS3 NP 350 NS1 NS2 NS3 Ratio 1: Ratio 2: Ratio 3:

R1 200 O R2 60 O R3 24 O

FIG. 52 Isolation transformer practice problems.

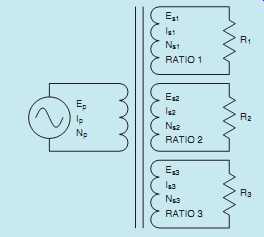
FIG. 53 Single-phase transformer with multi-secondaries.

PRACTICAL APPLICATIONS

1. You are working in an industrial plant. You must install a single-phase transformer. The transformer has the following information on the nameplate:

Primary voltage - 13,800 Secondary voltage - 240 Impedance - 5% kVA - 150 The secondary fuse has a blow rating of 800 A and an interrupt rating of 10,000 A. Is the interrupt rating sufficient for this installation?

2. You are working in an industrial plant.

An overhead crane is powered by 480 VAC. An electric brake on the hoist operates on 240 V. The brake has a current rating of 3.5 A. You have to install a transformer to reduce the 480 V to 240 V. The kVA rating of the transformer must be at least 115% greater than the expected load. The parts room has transformers of the following sizes: 0.025 kVA, 0.05 kVA, 0.1 kVA, 0.5 kVA, 1 kVA, 1.25 kVA, 1.5 kVA, and 2 kVA. Which of the available transformers should be used for this installation?