Guide to Small Electric Motors: Basic Magnetics

Electric motors convert electrical energy into mechanical energy by utilizing the properties of electromagnetic energy conversion. The different types of motors operate in different ways and have different methods of calculating the performance, but all utilize some arrangement of magnetic fields. Understanding the concepts of electromagnetics and the systems of units that are employed is essential to understanding electric motor operation. The first part of this Section covers the concepts and units and shows how forces are developed. Nonlinearity of magnetic materials and uses of magnetic materials are explained. Energy and coenergy concepts are used to explain forces, motion, and activation. Finally, this Section explains how motor torque is developed using these concepts.

1. UNITS

Although the rationalized mks system of units [Système International (SI) units] is used in this discussion, there are also at least four other systems of units-cgs, esu, emu, and Gaussian] that are used when describing electromagnetic phenomena.

These systems are briefly described as follows.

MKS. Meter, kilogram, second.

CGS. Centimeter, gram, second.

ESU. CGS with e0 = 1, based on Coulomb's law for electric poles.

EMU. CGS with µ0 = 1, based on Coulomb's law for magnetic poles.

Gaussian. CGS with electric quantities in esu and magnetic quantities in emu.

The factor 4p appears in Maxwell's equation.

Rationalized mks. µ0 = 4p× 10^-7 H/m, based on the force between two wires.

Rationalized cgs. µ0 = 1, based on Coulomb's law for magnetic poles. The factor 4p appears in Coulomb's law.

The rationalized mks and the rationalized cgs systems of units are the most widely used. These systems are defined in more detail in the following subsections.

1.1 The MKS System of Units

The rationalized mks system of units (also called SI units) uses the magnetic units tesla (T) and amps per meter (A/m), for flux density B and magnetizing force H, respectively. In this system, the flux density B is defined first (before H is defined), and is based on the force between two current-carrying wires. A distinction is made between B and H in empty (free) space, and the treatment of magnetization is based on amperian currents (equivalent surface currents).

Total or normal flux density B, T B =µ0 (H + M)

Intrinsic flux density Bi,T Bi =µ0M Permeability of free space µ0, (T·m)/A

µ0 = 4p× 10-7 Magnetization M,A/m M ==

Magnetic moment M, J/T m = MV = pl Magnetic pole strength p, A·m

1.2 The CGS System of Units

The rationalized cgs system of units uses the magnetic units of gauss (G) and oersted (Oe) for flux density B and magnetizing force H, respectively. In this system, the magnetizing force, or field intensity, H is defined first (before B is defined), and is

based on the force between two magnetic poles. No distinction is made between B and H in empty (free) space, and the treatment of magnetization is based on magnetic poles. The unit emu is equivalent to an erg per oersted and is understood to mean the electromagnetic unit of magnetic moment.

The magnetization or magnetic polarization Mis sometimes represented by the symbols I or J, and the intrinsic flux density Bi is then represented as 4pM, 4pI, or 4pJ.

1.3 Unit Conversions

2. DEFINITION OF TERMS

The Greeks discovered in 600 B.C. that certain metallic rocks found in the district of Magnesia in Thessaly would attract or repel similar rocks and would also attract iron. This material was called Magnes for the district of Magnesia, and is a naturally magnetic form of magnetite (Fe3O4), more commonly known as lodestone. Lode stone means "way stone," in reference to its use in compasses for guiding sailors on their way.

A bar-shaped permanent magnet suspended on a frictionless pivot (like a com pass needle) will align with the earth's magnetic field. The end of the bar magnet that points to the earth's geographic north is designated as the north magnetic pole and the opposite end is designated as the south magnetic pole. If any tiny compass needles are placed around the bar magnet, they will line up to reveal the magnetic field shape of the bar magnet. Connecting lines along the direction of the compass needles show that the magnetic field lines emerge from one pole of the bar magnet and enter the opposite pole of the bar magnet. These magnetic field lines do not stop or end, but pass through the magnet to form closed curves or loops.

By convention, the magnetic field lines emerge from the north magnetic pole and enter through the south magnetic pole. Two permanent magnets will attract or repel each other in an effort to minimize the length of the magnetic field lines, which is why like poles repel and opposite poles attract. Therefore, since the north magnetic pole of a bar magnet points to the earth's geographic north, the earth's geographic north pole has a south magnetic polarity.

Hans Oersted discovered in 1820 that a compass needle is deflected by an electric current, and for the first time showed that electricity and magnetism are related.

The magnetic field around a current-carrying wire can be examined by placing many tiny compass needles on a plane perpendicular to the axis of the wire. This shows that the magnetic field lines around a wire can be envisioned as circles centered on the wire and lying in planes perpendicular to the wire.

The direction of the magnetic field around a wire can be determined by using the right-hand rule, as follows (see Fig. 1).The thumb of your right hand is pointed in the direction of the current, where current is defined as the flow of positive charge from + to -.The fingers of your right hand curl around the wire to point in the direction of the magnetic field. If the current is defined as the flow of negative charge from - to +, then the left-hand rule must be used.

To summarize:

1. The north magnetic pole of a bar magnet will point to the earth's geographic north.

2. Magnetic field lines emerge from the north magnetic pole of a permanent magnet.

3. Magnetic field lines encircle a current-carrying wire.

4. Magnetic field lines do not stop or end, but form closed curves or loops that always encircle a current-carrying wire and/or pass through a permanent magnet.

5. The right-hand rule is used with current flowing from positive to negative and with the magnetic field lines emerging from the north magnetic pole.

2.1 System Performance

f= magnetic flux

NI = magnetomotive or magnetizing force

_ = reluctance

_ = permeance

?= flux linkage

FIG. 2 shows a magnetic circuit based on an electrical analogy. In general, a coil with N turns of wire and I amperes (amps) provides the magnetomotive force NI that pushes the magnetic flux f through a region (or a material) with a cross sectional area a and a magnetic flux path length l. In the electrical analogy, a voltage V provides the electromotive force that pushes an electrical current I through a region.

The amount of magnetomotive force required per unit of magnetic flux is called reluctance _.The amount of voltage required per amp is called resistance R.

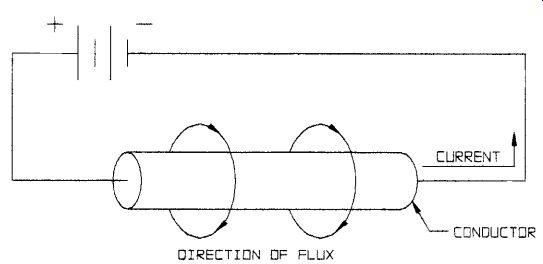
FIG. 1 Direction of flux.

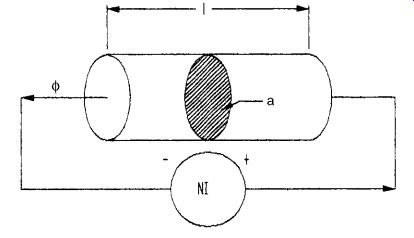
FIG. 2 Magnetic circuit with electrical analogy.

Visualization of Flux Linkage λ. FIG. 3 shows 10 magnetic flux lines passing through 4 turns of wire in a coil. Each turn of the coil is linked to the 10 magnetic flux lines, like links in a chain. Therefore, the total flux linkage ? is obtained by multiplying the turns N by the magnetic flux f, as defined in (Eq. 19). In this case, the magnetic flux linkage ?= 40 line turns, where the units of N are turns and the units of magnetic flux f are lines.

2.2 Material Properties

B = magnetic flux density

H = magnetic field intensity

µ= magnetic permeability The magnetic flux density B is defined as the magnetic flux per unit of cross-sectional area a. The magnetic field intensity H is defined as the magnetomotive force per unit of magnetic flux path l. The magnetic permeability µ of the material is defined as the ratio between the magnetic flux density B and the magnetic field intensity. The permeability can also be obtained graphically from the magnetization curve shown in Fig. 4. In the electrical analogy, the current density J, the electric field intensity E, and the electrical conductivity s are defined using ratios of similar physical parameters.

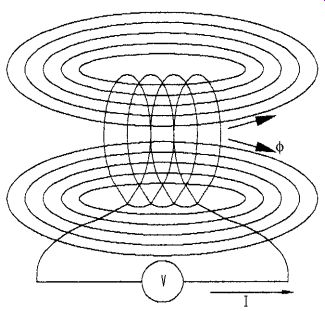
FIG. 3 Flux linkage visualization.

Electrical Analogy Permeability of free space, H/m or (T·m)/A:

.....where µ is the permeability of a material at any given point.

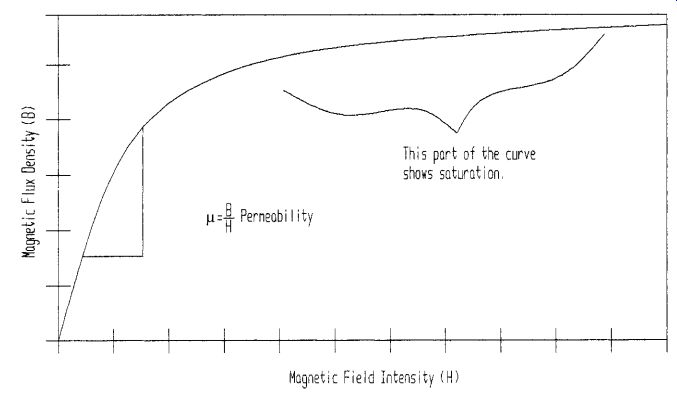
FIG. 4 Magnetization B-H curve showing permeability µ.

2.3 System Properties

_ = reluctance

_ = permeance

L = inductance

The reluctance _, as defined in (Eq. 17), can be written in a form based on the material properties and the geometry (µ, a, and l), as shown in (Eq. 29).

The same can be done for the permeance _, as shown in equation [1-30].

The inductance L is defined as the magnetic flux linkage ? per amp I, as shown in (Eq. 31).The inductance can be written in a form based on the material properties and the geometry (µ, a, and L), also shown in (Eq. 31).The B-H curve can be easily changed into a ?-I curve, as shown in Fig. 5, and the inductance can then be obtained graphically.

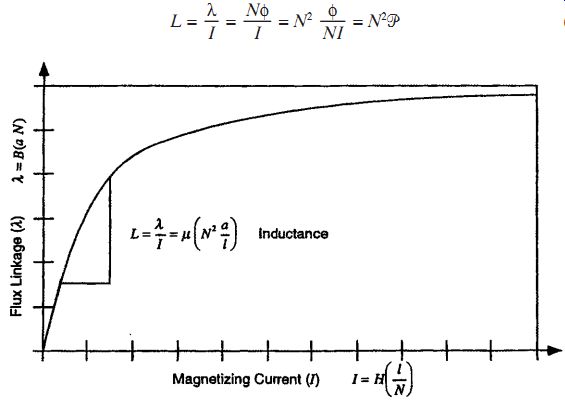
FIG. 5 Magnetization ?-I curve showing inductance L.

2.4 Energy

We = input electric energy

Wf = stored magnetic field energy

Wm = output mechanical energy

Wco = magnetic field coenergy

Energy Balance. All systems obey the first law of thermodynamics, which states that energy is conserved. This means that energy is neither created nor destroyed.

Therefore, an energy balance can be written for a general system stating that the change in energy input to the system ?We equals the change in energy stored in the system

?Wf plus the change in energy output from the system ?Wm.

This energy balance is illustrated in the following equation.

?We =?Wf +?Wm (Eq. 32)

Input Electric Energy We . The input electrical energy can be calculated by integrating the coil voltage and current over time, as follows.

Substituting Faraday's law, (Eq. 20), into (Eq. 33) shows that the input electrical energy is equal to the product of the coil magnetizing current I and the flux linkage ?.

Stored Magnetic Field Energy. As can be seen in Fig. 5, the flux linkage ? is a function of the magnetizing current I and depends on the material properties or the magnetization curve. The stored magnet field energy is calculated by integrating (Eq. 34) over the magnetization curve. By inspection of (Eq. 34), the area of integration lies above the magnetization curve, as shown in Fig. 6.

The stored magnetic field energy can be calculated for linear materials by substituting (Eq. 31) into (Eq. 34) as follows. Linear materials are characterized by a constant value of inductance L or permeability µ.

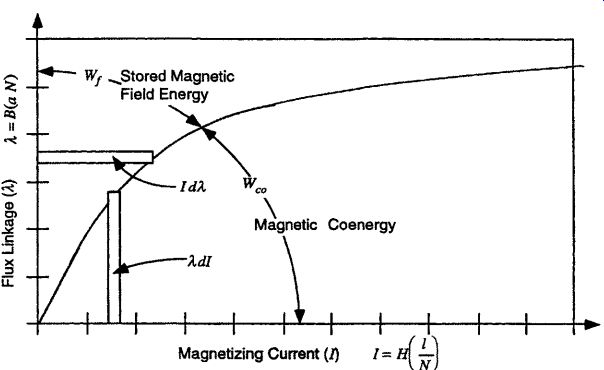
FIG. 6 Stored magnetic field energy and magnetic coenergy.

Output Mechanical Energy Wm. The change in mechanical energy ?Wm is equal to the product of the mechanical force F and the distance over which it acts ?X.

?Wm = F?X (Eq. 38)

In the limit as ?X ? 0, dWm = F dX (Eq. 39)

When a mechanical system includes a spring gradient k,

F = kX (Eq. 40)

Substituting (Eq. 40) into (Eq. 38) gives (Eq. 41); integrating gives (Eq. 42), the energy to change for a mechanical system with a linear spring.

Magnetic Coenergy Wco. The stored magnetic field energy Wf is derived from (Eq. 34), and is represented by the area above the magnetization curve as previously described and as shown in Fig. 7. The magnetic coenergy Wco is represented by the area under the curve, and can be derived by starting with (Eq. 34), as follows.

The magnetic coenergy can be calculated for linear materials by substituting (Eq. 31) into (Eq. 44) as follows. Linear materials are characterized by a constant value of inductance L or permeability µ:

where L and µ are constant.

A comparison of Eqs. (Eq. 37) and (Eq. 45) shows that the stored magnetic field energy Wf and the magnetic coenergy Wco are equal if the magnetic materials have linear properties:

?Wf =?Wco (Eq. 46) where L and µ are constant.

Electromechanical Energy Conservation (Mechanical Force, Torque). The mechanical forces and torques produced by electromagnetic actuators are derived using the energy balance from (Eq. 32).A graphical representation for the electro mechanical energy conversion is shown in Fig. 7 to help in visualizing the derivation. FIG. 7 shows two operating states for an electromagnetic actuator. State 1 is characterized by coil current I1, flux linkage ?1, and flux path length l1. State 2 is characterized by coil current I2 , flux linkage ?2 , and flux path length l2.The change in flux path length represents mechanical motion, which implies that there is a change in the mechanical energy. The change in the magnetization curve from flux path length l1 to l2 reflects a change in the inductance, as described in Eqs. (Eq. 30) and (Eq. 31).

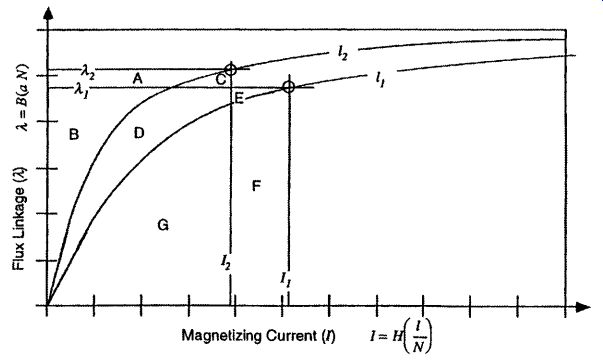
FIG. 7 Graphical visualization of electromechanical energy conversion.

The change in electric energy and the change in stored magnetic field energy are defined as follows.

The electric energy and the stored magnetic field energy for states 1 and 2 can be obtained by using the applicable regions above and below the magnetization curve designated as A, B, C,D, E, F, and G in Fig. 7.

The resulting change in the mechanical energy is obtained by rewriting the energy balance, (Eq. 32), and substituting the results from Eqs. (Eq. 52) and (Eq. 56), as follows.

2.5 Application of the Force and Energy Equations to an Actuator

The purpose of this section is to show how the energy and force equations can be applied to an actuator to determine the armature force. The reluctance actuator shown in Fig. 8a will be used for this discussion. The saturable iron regions of the actuator include the armature, which moves in the x direction, two stationary poles, and a coil core. The magnetic flux generally remains in the iron regions; however, it must cross air gap 1 and air gap 2 to reach the armature. Some of the magnetic flux finds alternative air paths which bypass the armature; these flux paths are called leakage flux paths. The air flux path shape and the reluctance equations are derived from the reluctance definition _ = 1/µa in Sec. 1.3.

The first step in constructing an equivalent reluctance model is to identify each iron flux path and each air flux path for the actuator. The iron flux paths include the core, pole 1, pole 2, and the armature, and the reluctances are designated as _core, _P1,_P2, and _arm, respectively. The air flux paths include gap 1, gap 2, leakage 1, and leakage 2, and the reluctances are designated as _g1, _g2, _L1, and _L2, respectively.

By observing the expected paths of the magnetic flux (Fig. 8a), an equivalent reluctance network can be assembled (Fig. 8b), in which each reluctance is modeled as an equivalent electrical resistor. The coil is shown as an amp-turn NI source in series with the core reluctance (Fig. 8b), and is modeled as an equivalent voltage source directed toward the left (from - to +), according to the right-hand rule. The magnetic flux f is modeled as an equivalent electric current.

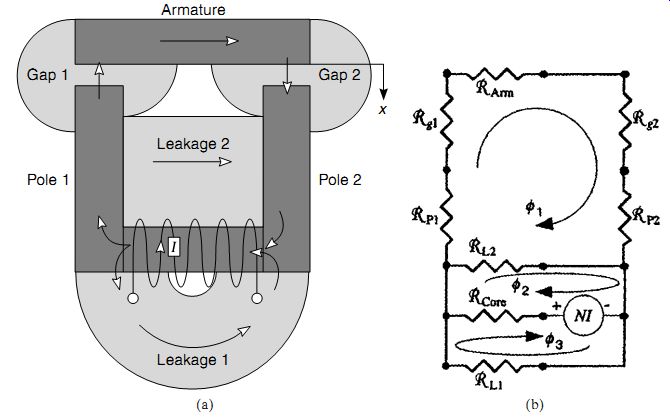
FIG. 8 (a) Actuator iron and air flux paths, and (b) equivalent reluctance network.

Three magnetic flux loops (f1, f2, f3) can be defined in the equivalent reluctance network (Fig. 8b). Three loop equations can be written in which all of the amp turn NI drops around each flux loop must sum to zero (magnetic Kirchoff's law), as follows.

[...]

This completes the solution for the state of the magnetic field in the actuator. The x-direction force on the armature can now be determined by calculating the change in the magnetic coenergy as a function of armature displacement in the x-direction.

The magnetic coenergy can be calculated for the entire actuator or for just the working air gaps.

Magnetic Coenergy Applied to the Entire Actuator. In general, the magnetic coenergy is calculated from (Eq. 44), which requires knowledge of the nonlinear magnetic properties in terms of the flux linkage ? and current I. However, the magnetic properties for ferromagnetic materials are normally published in terms of the magnetic flux density B and magnetic field intensity H, as B-H curves. By substitution of the definitions for flux linkage ?= Nf, magnetic flux density f= Ba, and magnetic field intensity NI = H1 into (Eq. 44), the magnetic coenergy can be calculated from the B-H property characteristics, as follows:

Iron is a ferromagnetic material and by definition it has nonlinear magnetic properties. Therefore, the magnetic coenergy in each of the iron reluctances must be calculated by integrating the area under the B-H curve, as follows. The total magnetic coenergy in the iron is the summation of the iron co-energies.

Air is not a ferromagnetic material, and by definition it has linear or constant magnetic properties. Therefore, the magnetic coenergy in each of the air reluctances is identical to the stored magnetic field energy (?Wf =?Wco).The magnetic coenergy in each of the air reluctances can be calculated from (Eq. 37), as follows. The total magnetic coenergy in the air is the summation of the air co-energies.

The armature force Farm can be obtained by calculating the total actuator magnetic coenergy Wco, tot at each of two armature positions, x1 and x2. The resulting armature force is the average force over the armature position change x = x1 to x2, and in the direction of the armature position change.

Magnetic Coenergy Applied to the Working Air Gaps. Since the armature force is produced across the working air gaps (gap 1 and gap 2), the armature force can be determined by considering the coenergy change in the working gaps alone. The total magnetic coenergy in the working air gaps is the summation of the air gap coenergies from Eqs. (Eq. 99) and (Eq. 100), as follows:

The armature force Farm can be obtained by calculating the total working air gap magnetic coenergy Wco, gap at each of two armature positions x1 and x2.The resulting armature force is the average force over the armature position change x = x1 to x2, and in the direction of the armature position change.

2.6 Summary of Magnetic Terminology

The analysis and design of electromagnetic devices can be accomplished by using the relations presented in Secs. 2.1 to 2.4. The key equations from these sections are listed here.

System Performance Magnetic Ohm's law

3. ESTIMATING THE PERMEANCE OF PROBABLE FLUX PATHS

Defining the permeance of the steel parts is very simple because the field is generally confined to the steel. Therefore, the flux path is very well defined because it has the same geometry as the steel parts.

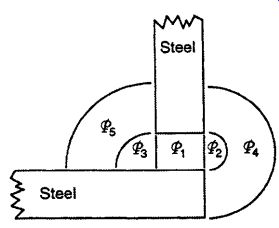
FIG. 9 Air gap permeance paths.

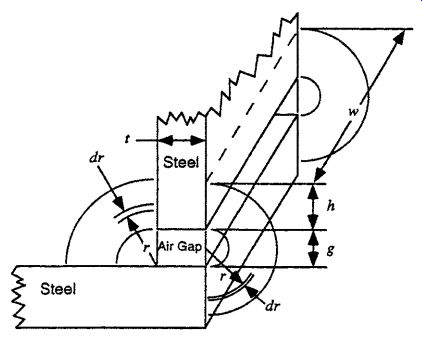
FIG. 10 Air gap and steel part dimensions.

FIG. 11 Magnetic flux lines illustrated by iron filings on U-shaped magnet.

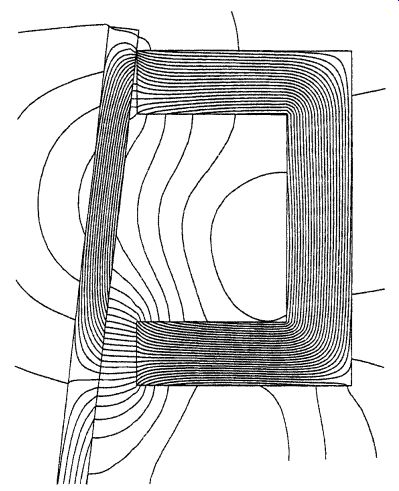
FIG. 12 Magnetic flux lines illustrated by a finite element solution flux-line plot on a U-shaped magnet.

The flux path through air is complex. In general, the magnetic flux in the air is perpendicular to the steel surfaces and spreads out into a wide area. As an example, Fig. 9 shows five of the flux paths for a typical air gap between two pieces of steel. The total permeance of the air gap is equal to the sum of the permeances for the parallel flux paths.

The permeance of each path can be calculated based on the dimensions shown in Fig. 10 and on (Eq. 30), as follows. Path _1 is the direct face-to-face flux path. Paths _2,_3, _4, and _5 are generally identified as fringing paths. H. C. Roters (1941) recommends that the value for dimension h, as shown in Fig. 10, should be equal to 90 percent of the smaller thickness of the two steel parts, h = 0.9t. However, it is easier to remember the slightly larger value of h = 1.0t, and there is no significant loss in accuracy. Two examples of magnetic flux lines are shown in Fig. 11 (iron filings on a U-shaped magnet) and Fig. 12 (finite element result flux-line plot). In these examples it is easy to see the general flux path shapes shown in Fig. 9.

Path _1. The direct face-to-face air gap flux path has the same geometry as the perpendicular interface region between the two steel parts.

Path _2 (Half Cylinder). The cross-sectional area of this flux path varies along the length of the path. Therefore, (Eq. 30) is modified as follows, where v2 is the volume of flux path _2. Roters (1941) uses a graphical approximation to the mean path length, resulting in a permeance with a value of _2 = 0.26 µ0w, which is slightly larger than that shown here.

Path _3 (Quarter Cylinder). This flux path is very similar to flux path _2, and the calculation method is identical. Roters (1941) uses a graphical approximation to the mean path length, resulting in a permeance with a value of _3 = 0.52 µ0w, which is slightly larger than that shown here.

Path _4 (Half Cylindrical Shell). The cross-sectional area of this flux path is constant. However, the magnetic flux path length increases as the radius r increases.

Therefore, (Eq. 30) is written in differential form and the permeance is calculated

by integrating over the radius as follows. Roters (1941) uses the same procedure and shows the same results.

Path _5 (Quarter Cylindrical Shell). This flux path is very similar to flux path _4, and the calculation method is identical. Roters (1941) uses the same procedure and shows the same result.

Paths _6 and _7. There are additional flux paths that extend into and out of the page in Fig. 9. Based on the geometry shown in Fig. 10, there is a half-cylinder flux path (_6) extending out of the page over path _1 and into the page behind path _1, which is identical in shape to path _2. There is also a half cylindrical shell flux path (_7) extending out of the page over path _6 and into the page behind path _6, which is identical in shape to path _4. The values for flux paths _6 and _7 can be obtained from Eqs. (Eq. 121) and (Eq. 131) by using the proper dimensions for the flux paths from Fig. 10, as follows.

Path _8 (Spherical Octant). There are also spherical flux paths on the corners, as shown in Fig. 13. The permeance of these flux paths can be estimated using the same technique demonstrated for evaluating flux paths _2 through _5, as follows.

The cross-sectional area of flux path _8 varies along the path length. Therefore, (Eq. 30) is modified as follows, where v8 is the volume of flux path _8.Roters (1941) uses a graphical approximation to the mean flux path length, resulting in a permeance with a value of _8 = 0.308 µ0g, which is slightly smaller than that shown here.

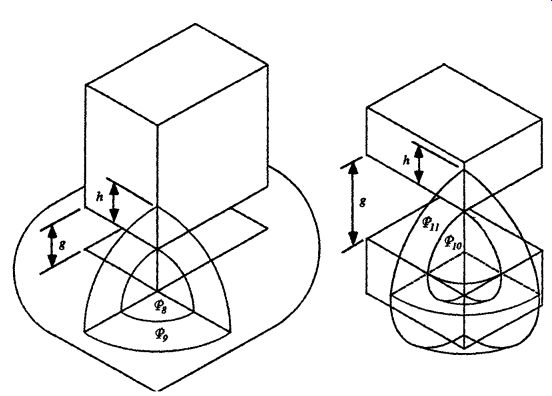
FIG. 13 Corner flux paths in the shape of spherical octants and quadrants.

Path _9 (Spherical Shell Octant). The cross-sectional area of this flux path varies along the path length, and the magnetic flux path length increases as the radius increases. Therefore, (Eq. 30) is written in differential form, and the permeance is calculated by integrating over the radius as follows, where v9 is the volume of flux path _9.Roters (1941) uses a graphical approximation to both the mean path length and the mean path area, resulting in a permeance with a value of _9 = 0.50µ0h, which is slightly smaller than that shown here.

Path _10 (Spherical Quadrant). The cross-sectional area of this flux path varies along the path length. Therefore, (Eq. 30) is modified as follows, where v10 is the volume of flux path _10. Roters (1941) uses a graphical approximation to the mean path length, resulting in a permeance with a value of _10 = 0.077 µ0g, which is slightly smaller than that shown here.

Path _11 (Spherical Shell Quadrant). The cross-sectional area of this flux path varies along the path length, and the magnetic flux path length increases as the radius increases. Therefore, (Eq. 30) is written in differential form, and the permeance is calculated by integrating over the radius as follows, where v9 is the volume of flux path _9. Roters (1941) uses a graphical approximation to both the mean path length and the mean path area, resulting in a permeance with a value of _9 = 0.25

µ0h, which is slightly smaller than that shown here.

Total Permeance. The total permeance of the air gap is equal to the sum of the individual parallel flux paths, as follows:

_total = _1 + _2 + _3 + _4 + _5 + 2(_6 + _7) + 4(_8 + _9 + _10 + _11) (Eq. 164)

3.1 Summary of Flux Path Permeance Equations

All of the flux path permeances are based on (Eq. 30).The relationships shown here are for the special case of 90° and 180° angles between steel surfaces. However, the techniques that are demonstrated here can be applied to any geometry. The final forms of the flux path permeances for Figs. 9, 10, and 14 follow. All of the magnetic flux paths represent fringing regions except for the direct face-to-face flux path (_1).

Direct face-to-face flux path (Figs. 9 and 10)

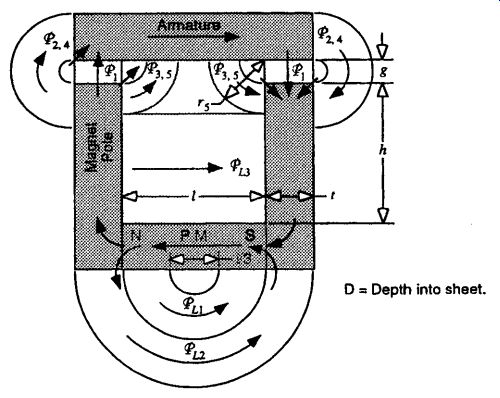
FIG. 14 Two-dimensional air flux paths around a permanent mag net reluctance actuator._L1,_L2, and _L3 are leakage flux paths._2,_3,_4, and _5 are fringing flux paths (also shown in Fig. 9).

3.2 Leakage Flux Paths

The magnetic flux paths shown in Figs. 9, 10, and 13 (the direct face-to-face flux path _1 and the fringing flux paths _2,_3,_4, and _5) are based on the air gap geometry. These flux paths carry the magnetic flux across the working gaps g from the magnet poles to the armature, as shown for the permanent-magnet reluctance actuator in Fig. 14. Also shown are the leakage flux paths _L1,_L2, and _L3,which carry the magnetic flux between the magnet poles, and prevent some of the magnetic flux from reaching the armature and the working gaps g. The effect of each flux path is described here.

Direct Face-to-face Flux Path (_1). This flux path is the highest-efficiency producer of the force on the armature. It also produces the majority of the force on the armature. The total magnetic flux through this path is limited by the saturation flux for the materials in the magnet poles and the armature.

Fringing Flux Paths (_2, _3, _4, and _5). The fringing flux paths increase the sys tem permeance, increase the total magnetic flux, and produce a lower-efficiency force on the armature than does the direct flux path. Initial magnetic performance estimates commonly use only the direct face-to-face flux path and ignore the fringing flux paths, in order to make the first calculations very easy and fast. If the steel in the magnet poles and armature is not saturated, then the fringing flux paths increase the total magnetic flux and increase the armature force. If the steel in the magnet poles and armature is saturated, then adding the fringing flux paths does not change the total magnetic flux, and since the fringing flux paths take magnetic flux away from the direct flux path, the armature force is decreased.

Leakage Flux Paths (_L1, _L2, and _L3). These flux paths take magnetic flux away from both the direct flux path and the fringing flux paths, and produce no force on the armature. Also, the magnetic flux carried by the leakage flux paths must be carried by a portion of the magnet poles. This causes the magnet pole material to reach the saturation flux limit sooner than expected. Therefore, the leakage flux paths cause a large decrease in the armature force. When a permanent magnet is placed near the working gap, the armature force is increased, because some of the leakage flux becomes fringing flux. This essentially minimizes the leakage flux. Conversely, the leakage flux paths are useful in permanent-magnet systems as a means of protecting the permanent magnet from large demagnetizing fields. In this case, some of the demagnetizing flux bypasses the permanent magnet through the leakage flux paths.

The leakage flux paths can be evaluated by using the following procedures.

Path _L1 (Half Cylindrical Shell). This flux path is identical in shape to path _4.

The diameter of the internal half cylindrical shell d1 is equal to 33 percent of the permanent-magnet length. The radius of the external half cylindrical shell r1 is equal to 50% of the permanent-magnet length. These permeance relationships are shown here, based on Eqs. (Eq. 126) through (Eq. 131).This flux path is valid only for alnico and earlier permanent magnets, which have effective poles at 70 percent of the magnet length. Ferrite and rare-earth permanent magnets have effective poles at 95 percent of the magnet length; therefore, no magnetic flux is generated in this path and the permeance is zero.

Path _L2 (Half Cylindrical Shell). This flux path is also identical in shape to path _4. The dimensions can be obtained by inspection from Fig. 14, and the permeance relationships shown here are based on Eqs. (Eq. 126) through (Eq. 131).

Path _L3 (Direct Pole-to-Pole). This flux path is identical in shape to path _1. The lower edge of the path is located at the permanent magnet. The upper edge of the path is located at a distance equal to radius r5 below the armature. Radius r5 is defined by equating the length of a flux line along the radius to 50 percent of the length of a flux line in the leakage flux path _L3. These permeance relationships are shown here, based on Eqs. (Eq. 114) through (Eq. 116):

[...] for a permanent magnet.

If the permanent magnet is replaced with a coil, then this path has only half of this permeance. The magnetic flux at the bottom of the flux path encircles zero coil amp-turns, and the magnetic flux at the top of the flux path encircles all of the coil amp-turns. Therefore, a coil actuator contains only 50 percent of the magnetic flux in path _L3 as compared to a permanent-magnet actuator. This corresponds to a 50 per cent permeance value for the coil actuator.

For a coil:

Total Permeance and Equivalent Reluctance Circuit. The total reluctance of the armature air gaps (_1, _2, _3, _4, and _5) and the leakage flux paths (_L1, _L2, and _L3), as seen from the permanent magnet, can be calculated by drawing the equivalent reluctance network, as shown in Fig. 15.The permeance of each armature air gap is the sum of the air gap permeances.

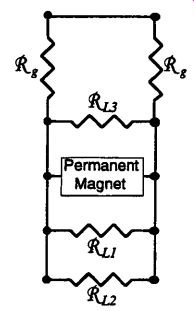
FIG. 15 Equivalent reluctance network for the permanent magnet leakage shown in Fig. 14.

4. ELECTROMECHANICAL FORCES AND TORQUES

The mechanical force and torque equations, Eqs. (Eq. 68) and (Eq. 73), are general equations which can be applied to an entire system or individually to a specific air gap.

When these equations are applied to a nonlinear system, the coenergy Wco must be obtained by integrating each region over the local magnetization curve:

for constant L, µ.

Equations (Eq. 74) and (Eq. 75) can be applied to a specific air gap to obtain the mechanical force or torque. The magnetic medium in the air gap is linear. Therefore, the coenergy Wco and the stored field energy Wf are equal and can be obtained from (Eq. 37), where NI is the magnetizing force in the air gap, f is the magnetic flux passing across the air gap, and _ is the air gap permeance.

The total magnetizing force provided by the coil NI coil is used to magnetize both the steel part and the air gaps. In general, the magnetizing force in the steel parts is small, and the resulting magnetizing force in the air gap NI is nearly equal to the coil magnetizing force (NI ˜ Icoil).However, when the steel parts become saturated, the magnetizing force in the steel parts becomes large and the magnetizing force in the air gap becomes small (NI _NIcoil).The saturation of the steel parts produces a magnetic flux limiting condition in which the second form of Eqs. (Eq. 74) and (Eq. 75) can be used effectively.

4.1 General Air Gap Linear Equations

An actuator or motor generally has one or two magnetizing sources. Some examples are listed here.

_ A reluctance motor has one stationary coil and a moving armature that changes the reluctance _ or the permeance _ of the air gap as it moves. The mechanical force is generated by the change in reluctance.

_ A flux-transfer reluctance motor has two stationary coils and a moving armature that changes the reluctance _ or the permeance _ of the air gap as it moves. The mechanical force is generated by the change in reluctance. Usually one of the stationary coils provides a constant magnetizing force to produce a bias magnetic field which is modified by the second coil. The coil that produces the constant magnetizing force can be a permanent magnet.

_ A moving coil motor has one moving coil that changes the number of turns which contribute to the total magnetizing force in the motor. There may be a second coil (stationary) that provides a constant magnetizing force to increase the air gap stored magnetic field energy and the resulting force or torque. The second coil can be replaced by a permanent magnet. The permanent magnet and coil can be interchanged to produce a moving magnet motor. The mechanical force is generated by the change in the number of turns and is also called the Lorentz force.

The magnetizing force NI in Eqs. (Eq. 74) and (Eq. 75) is expanded here to show the contribution from a second coil NaIa (either stationary or on a moving armature) and the contribution from a bias field coil NfIf (stationary).

Multiplying by the permeance gives the energy expression needed in Eqs. (Eq. 74) and (Eq. 75).Also, the definition of the self-inductance of the moving armature coil La, the self-inductance of the bias field coil Lf, and the mutual inductance of both coils L can be substituted into (Eq. 188) as follows:

The first term in Eqs. (Eq. 203) and (Eq. 204) represents the reluctance force produced by a change in air gap permeance as a function of the armature position. The second term represents the Lorentz force on the moving coil due to the interaction with the magnetic flux produced by the armature coil (this is typically called the armature reaction force). The third term represents the Lorentz force on the moving coil due to the interaction with the magnetic flux produced by the bias field coil.

4.2 Reluctance Actuators with Small Air Gaps and Saturation

When an air gap is very small, the permeance _1 becomes very large in comparison to the fringing flux paths _2 through _10.Therefore, the total permeance _total can be closely approximated by the direct face-to-face permeance _1, (Eq. 30).

Reluctance Normal Force. The force for the actuator in Fig. 16 can be written as follows, based on Eqs. (Eq. 203) and (Eq. 30). The motion of the armature X is defined to be in the direction to close the air gap, and the initial length of the air gap is defined to be g0. Also, Na = Ia = 0 because there is only one coil. The area of the pole face is a =TPD.

This is the permeance of the flux path between one pole and the armature. The total permeance of the flux path includes two air gap permeances in series. There fore, the total permeance _T is equal to one-half of the permeance for one air gap:

for small g and limited NI.

All of the variables in (Eq. 209) are constant except the armature position g.

Therefore, the armature reluctance force is proportional to the inverse square of the armature position (or to the size of the working air gap). If the steel parts become saturated in some armature positions, then the air gap magnetizing force is reduced.

Under this condition the air gap magnetizing force is a function of the armature position.

When the steel parts become saturated the total magnetic flux f in the system reaches a maximum limit, as shown in Fig. 4. (Eq. 209) can be written as follows by substituting Eqs. (Eq. 18), (Eq. 21), and (Eq. 30):

FIG. 16 Actuator with reluctance force produced normal to the armature bottom surface, in the direction of motion X.

... for small g and limited f and B.

All of the variables in (Eq. 211) are constant. Therefore, the armature reluctance force is constant regardless of the armature position when the system is saturated. Due to symmetry, the force on each side of the armature or on each pole of the magnet frame is half of the total force, as shown here:

F = (Eq. 212)

... for a single pole, where g is small.

Maximum Possible Reluctance Normal Force. The reluctance normal force in (Eq. 212) can be divided by the pole area a to obtain the normal magnetic pressure p on the pole, as shown in (Eq. 213). The maximum normal magnetic pressure is dependent only on the saturation magnetic flux density (for small gaps). Steel typically saturates at 1.60 T. Therefore, the maximum possible normal magnetic pressure for this steel is 150 lb/in^2:

... for a single pole, where g is small.

This relationship can be converted into the following simple design strategy. If 150 lb of magnetic force is required, then at least 1.0 in2 of steel is needed. Conversely, if we are limited to 1.0 in^2 of steel, then the maximum possible magnetic force will be 150 lb.

Reluctance Tangential Force. The force for the actuator in Fig. 17 can be written as follows, based on Eqs. (Eq. 203) and (Eq. 30).The motion of the armature x is defined to be in the direction to insert the armature into the stator cup. Also, Na = Ia = 0 because there is only one coil:

........where C is small and NI is limited.

All of the variables in (Eq. 218) are constant. Therefore, the armature reluctance force is constant regardless of the armature position. If the steel parts become saturated in some armature positions, then the air gap magnetizing force is reduced.

Under this condition, the air gap magnetizing force is a function of the armature position, and a new air gap magnetizing force must be calculated at each position.

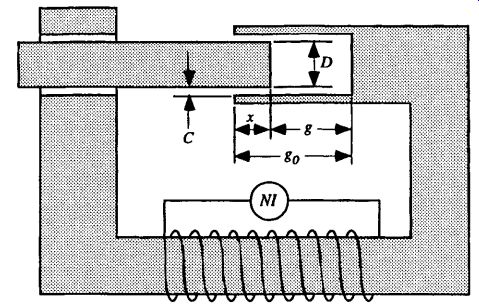
FIG. 17 Actuator with reluctance force produced tangential to the armature side surface, in the direction of motion x.

When the steel parts become saturated, the total magnetic flux f in the system reaches a maximum limit, as shown in Fig. 4. (Eq. 218) can be rewritten as follows by substituting Eqs. (Eq. 18) and (Eq. 30):

... where C is small and f is limited.

All of the variables in (Eq. 220) are constant except for the armature position x. Therefore, the armature reluctance force is inversely proportional to the square of the armature position when the system is saturated. (Eq. 221) is the flux density B limited form of (Eq. 220),which was obtained by substituting Eqs. (Eq. 21) and (Eq. 215) into (Eq. 220). (Eq. 221) shows that the force is independent of the armature position x as long as the air gap flux density B is constant. The force is constant, and the air gap flux density is constant if the actuator steel parts are not saturated:

...........where C is small and B is limited.

Pole Shaping. An example of the performance variations that are possible by shaping the pole faces can be observed by comparing Eqs. (Eq. 209) and (Eq. 218) and Figs. 16 and 17.The normal force on the pole faces shown in Fig. 16 and (Eq. 218) is inversely proportional to the square of the armature position, F ? 1/g^2.

The tangential force F on the pole faces shown in Fig. 17 and (Eq. 209) is constant regardless of the armature position. A force characteristic between these two limiting conditions can be achieved by using a cup-cone configuration. Fig. 16 is similar to the limiting configuration of a flat-face cone, and Fig. 17 is similar to the limiting configuration of a straight-sided cup. Therefore, it is possible to shape the force characteristic as a function of the armature position by modifying the pole face, as shown in Fig. 18.

Reluctance Tangential Torque. The torque for the actuator in Fig. 19 can be writ ten as follows, based on Eqs. (Eq. 204) and (Eq. 30). The motion of the armature ? is defined to be in the direction to align the armature vertically with the stator poles.

Also, Na = Ia = 0 because there is only one coil:

... where g is small and NI is limited.

All of the variables in (Eq. 227) are constant. Therefore, the armature reluctance torque is constant regardless of the armature position. If the steel parts become saturated in some armature positions, then the air gap magnetizing force is reduced.

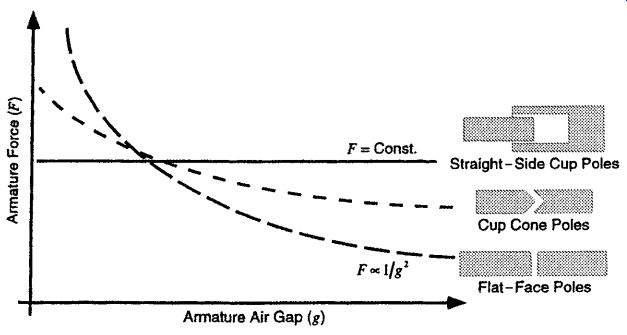
FIG. 18 Force curve performance variations due to modification of the pole shape.

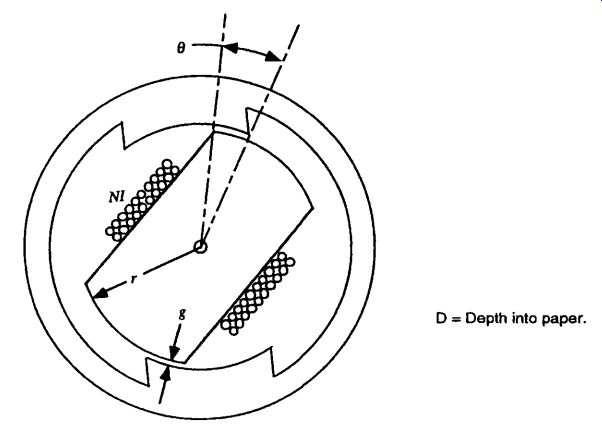
FIG. 19 Actuator with reluctance torque produced tangential to the armature end surface, in the direction of motion ?.

When the steel parts become saturated, the total magnetic flux f in the system reaches a maximum limit, as shown in Fig. 4. (Eq. 218) can be rewritten as follows by substituting Eqs. (Eq. 18) and (Eq. 30):

... where C is small and f is limited.

All of the variables in (Eq. 220) are constant except for the armature position x. Therefore, the armature reluctance force is inversely proportional to the square of the armature position when the system is saturated. (Eq. 221) is the flux density B limited form of (Eq. 220),which was obtained by substituting Eqs. (Eq. 21) and (Eq. 215) into (Eq. 220). (Eq. 221) shows that the force is independent of the armature position x as long as the air gap flux density B is constant. The force is constant, and the air gap flux density is constant if the actuator steel parts are not saturated:

F =pDC (Eq. 221) where C is small and B is limited.

Pole Shaping. An example of the performance variations that are possible by shaping the pole faces can be observed by comparing Eqs. (Eq. 209) and (Eq. 218) and Figs. 16 and 17. The normal force on the pole faces shown in Fig. 16 and (Eq. 218) is inversely proportional to the square of the armature position, F ? 1/g^2. The tangential force F on the pole faces shown in Fig. 17 and (Eq. 209) is constant regardless of the armature position. A force characteristic between these two limiting conditions can be achieved by using a cup-cone configuration. Fig. 16 is similar to the limiting configuration of a flat-face cone, and Fig. 17 is similar to the limiting configuration of a straight-sided cup. Therefore, it is possible to shape the force characteristic as a function of the armature position by modifying the pole face, as shown in Fig. 18.

Reluctance Tangential Torque. The torque for the actuator in Fig. 19 can be writ ten as follows, based on Eqs. (Eq. 204) and (Eq. 30). The motion of the armature ? is defined to be in the direction to align the armature vertically with the stator poles.

Also, Na = Ia = 0 because there is only one coil:

FIG. 18 Force curve performance variations due to modification of the pole shape.

........where g is small and NI is limited.

All of the variables in (Eq. 227) are constant. Therefore, the armature reluctance torque is constant regardless of the armature position. If the steel parts become saturated in some armature positions, then the air gap magnetizing force is reduced.

FIG. 19 Actuator with reluctance torque produced tangential to the armature end surface, in the direction of motion ?.

Under this condition the air gap magnetizing force is a function of the armature position, and a new air gap magnetizing force must be calculated at each position.

When the steel parts become saturated, the total magnetic flux f in the system reaches a maximum limit, as shown in Fig. 4. (Eq. 227) can be rewritten as follows by substituting Eqs. (Eq. 18) and (Eq. 30):

... where g is small and f is limited.

All of the variables in (Eq. 229) are constant except for the armature position ?. Therefore, the armature reluctance torque is inversely proportional to the square of the armature position when the system is saturated. Again, as shown in the previous section, the torque produced at each end of the armature is one-half of the total torque:

T = (Eq. 230) where g is small and f is limited.

(Eq. 231) is the flux density B limited form of (Eq. 230), which was obtained by substituting Eqs. (Eq. 21) and (Eq. 223) into (Eq. 230). (Eq. 231) shows that the torque is independent of the rotation angle ? as long as the air gap flux density B is constant. The torque is constant, and the air gap flux density is constant if the actuator steel parts are not saturated:

.....where g is small and B is limited.

Moving-Coil Actuator Lorentz Force.

The force for the moving-coil actuator in Fig. 20 can be written as follows, based on Eqs. (Eq. 203) and (Eq. 30).The motion of the armature X is defined to be in the direction to bring more of the moving coil into the magnetic circuit. Also, _ is constant, because the size of the air gap does not change as the position of the moving coil changes. Therefore, the rate of change of the permeance with respect to the armature position is zero.

d = 0 (Eq. 232)

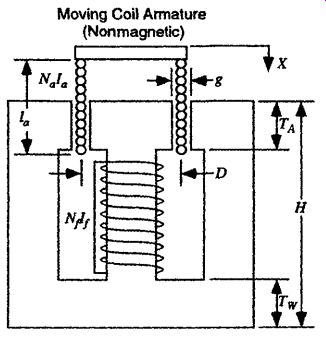
FIG. 20 Moving-coil actuator producing a Lorentz force in the direction of motion X.

The length of wire on the moving coil that is in the air gap permeance path can be calculated as follows. The permeance is based on the direct face-to-face flux path with the assumption of a small gap.

The rate of change of the turns in the moving coil with respect to the moving-coil position is calculated by dividing the number of turns in the moving coil by the length of the moving coil, as follows.

The total magnetic flux across the moving coil in the small air gap is equal to the magnetic flux from the bias field fa plus the magnetic flux from the moving coil ff.

The total magnetic flux density B across the moving coil in the small air gap can also be calculated as shown here.

Substituting Eqs. (Eq. 232), (Eq. 233), (Eq. 234), and (Eq. 235) into (Eq. 203) gives the following moving-coil force characteristic, known as the Lorentz force.

Reluctance Normal Torque. The torque for the actuator shown in Fig. 21 can be written as follows, based on Eqs. (Eq. 204) and (Eq. 30).The motion of the armature ? is defined to be in the direction to open the air gap g. Since the air gap thickness varies as a function of the radius from the pivot point, the equations are written in differential form.

The permeance of the flux path between each pole and the armature is obtained by integrating over the entire pole face.

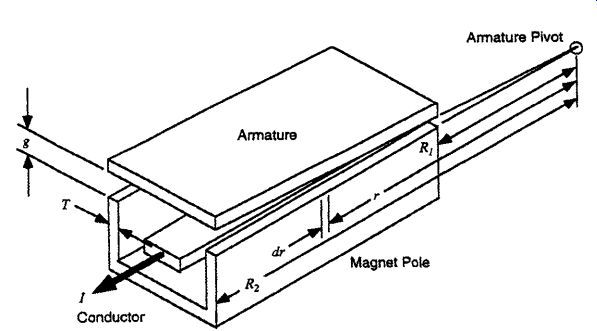
FIG. 21 Actuator with reluctance torque produced normal to the armature bottom surface, in the direction of motion ?.

Differentiating the permeance with respect to the armature position and substituting the result into (Eq. 204) gives the total torque on the armature.

The location of the force centroid on the armature can be obtained by dividing the total armature torque, (Eq. 246), by the total force on the armature. The total armature force is calculated by integrating the differential force over the radial length of the armature, as follows. The first step is to convert the permeance equation (Eq. 242) into linear coordinates.

Dividing the torque equation (Eq. 246) by the force equation (Eq. 253) gives the position of the force centroid.

5. MAGNETIC MATERIALS

Magnetic materials are generally divided into two categories, soft materials and hard materials. The soft magnetic materials are easy to magnetize and demagnetize; they have high permeability and low losses. The hard magnetic materials are difficult to magnetize and demagnetize. Therefore, the hard magnetic materials are generally referred to as permanent magnets.

Permanent magnets were initially made from quench-hardened steels. Some references suggest that good permanent-magnet steel was available from China as early as 500 A.D. These permanent-magnet steels, which were initially made from plain carbon steel, steadily progressed to highly alloyed cobalt steels with a carbon content as high as 1.2 percent by 1920.These permanent-magnet steels are mechanically very hard materials, with Brinell hardness values as high as 690.

High-permeability low-loss materials are made from very low carbon annealed steels. These low-alloy annealed steels are mechanically very soft materials, with Brinell hardness values as low as 130.

The permanently magnetic materials became known as hard magnetic materials, and the high-permeability low-loss materials became known as soft magnetic materials, with the terms soft and hard referring to the mechanical hardness of the material. The following sections describe the material properties for both the soft and hard materials.

The electrons in the atoms of materials circulate around the atoms in orbits, creating an orbital magnetic field. The electrons also spin on their own axes, producing a spin magnetic field. In most materials, there are other electrons which cancel these magnetic fields. However, magnetic materials such as iron, nickel, and cobalt have lone electrons which contribute a net magnetic field to each atom. Groups of atoms with the same magnetic field direction are called domains. Also, groups of atoms that form into one continuous crystal structure are called grains. In general, there are approximately 10^15 atoms in a domain, 10^6 domains in a grain, and 10^2 grains in a cubic centimeter.

During magnetization of some materials, the domain boundaries (or walls) move, so that the aligned domains become larger and the misaligned domains become smaller. If the magnetic material contains alloying elements, such as in the case of the quench-hardened permanent-magnet steels, nonmagnetic carbide inclusions are formed in the grain boundaries. The motion of a domain boundary through a non magnetic inclusion requires more energy, and this makes it more difficult to magnetize and demagnetize the permanent-magnet steels.

In other materials, the domain walls are pinned at the grain boundaries by car bide or other intermetallic compounds. If the energy required to move the domain wall is not exceeded during magnetization, the domain wall will remain pinned, and the entire domain will rotate to align with the magnetizing field.

5.1 Soft Magnetic Materials

Soft magnetic materials typically have a very narrow magnetic hysteresis loop to minimize losses and to maximize the permeability µmax, as shown in Fig. 22.

(Eq. 37) and Fig. 6 show that the area within the hysteresis loop represents energy. When ac coils and motors drive the magnetic material around the hysteresis loop, energy is lost in the form of heat. Therefore, minimizing the width of the hysteresis loop (coercive force Hc) will also minimize the hysteresis loss. The maximum slope of the hysteresis loop µmax is approximately equal to the ratio of the remnant flux density Br to the coercive force Hc. Therefore, minimizing the width of the hysteresis loop (coercive force Hc) will also maximize the permeability µmax.

FIG. 22 Magnetic hysteresis loop and characteristic parameters.

The magnetic permeability µmax reflects the ability of a material to carry magnetic flux. As mentioned, steel materials are composed of uniform magnetic regions called domains. When a magnetic field intensity is applied to a steel material, the magnetic domains rotate to align with the magnetic field. As the magnetic field intensity is increased, additional domains rotate into alignment with the magnetic field. Residual stress adds energy to the crystal structure and prevents the domains from rotating. The result is an increase in coercive force.

Small coercive force values are typically obtained in steels by minimizing the car bon content and by eliminating the residual strain with a full anneal. The properties of various soft magnetic materials are listed in Table 1.1.

5.2 Hard Magnetic Materials (Permanent Magnets)

Hard magnetic materials (permanent magnets) typically have a very wide magnetic hysteresis loop to maximize the operating magnetic field energy, as shown in Fig. 23. Permanent magnets are magnetized in quadrants I and III and are used in magnetic devices in quadrants II and IV. Since quadrants II and IV are identical, the properties and performance characteristics described here are based on quadrant II.

Both the normal and intrinsic hysteresis loops are shown in Fig. 23. Most permanent-magnet specification sheets show both curves, and both curves are required to fully determine the permanent-magnet performance at different temperatures. However, in general, only the normal curve is required to determine the performance of the permanent magnet and the system at constant temperature.

The intrinsic curve represents the added magnetic flux that the permanent magnet material produces. The normal curve represents the total measurable or usable magnetic flux which is carried in combination by the air (free space) and by the permanent-magnet material. For example, imagine that a coil is placed in air with a flux meter located at one end of the coil axis. The magnetic flux measured by the meter is the flux carried by the air, and is called the air flux. When a magnetic material is placed in the center of the coil, the magnetic flux increases. The amount of the increase is called the intrinsic flux, and the total of the air flux plus the intrinsic flux is called the normal flux. The total or normal flux is the new flux-meter reading.

The quadrant II operating region generally lies on the normal curve between the remnant flux density Br and the coercive force Hc. As the external system acts to demagnetize the permanent magnet, the operating point will move from Br toward Hc. As the external system acts to magnetize the permanent magnet, the operating point will move from Hc toward Br. As long as the operating point remains on the linear slope of the normal curve between the Br and Hc points, the magnetizing and demagnetizing cycles will be reversible. However, if the demagnetizing field becomes large enough to move the operating point beyond the linear region toward the Hc point, the subsequent magnetizing cycle will follow a different return path.

For example, if the demagnetizing field becomes large enough to move the operating point beyond the coercive force Hc point to the recoil point, the ensuing magnetizing cycle will follow the recoil line at a slope of µrev rather than return up the nonlinear demagnetizing path toward the Hc point. The magnetizing and demagnetizing cycles will then be reversible along the linear recoil line.

TABLE 1 Soft Magnetic Material Properties

Permanent magnets are almost always designed to operate on the linear region between the remnant flux density Br and the coercive force Hc. The position of the operating point can be identified by the pair of coordinates (Bd, Hd), the demagnetizing flux density and field intensity. The product BdHd is called the energy product and represents the energy supplied to the system from the permanent magnet. The maximum energy product BH max is a relative measure of the strength of a permanent magnet and is always listed on the material specification sheet.

Typical Properties of Permanent Magnets. Some typical properties of common permanent-magnet materials are listed in Table 1.2, and the quadrant II normal curves are plotted in Fig. 24.There are obvious design and performance tradeoffs involved in selecting a permanent-magnet material, including the shape of the nor mal curve, the energy product, and the operating temperature.

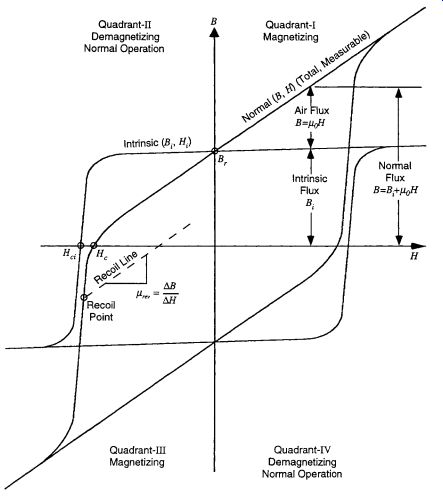
FIG. 23 Hard magnetic material hysteresis loop and characteristic parameters.

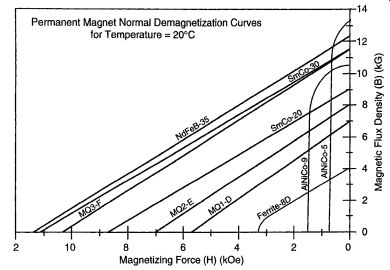
FIG. 24

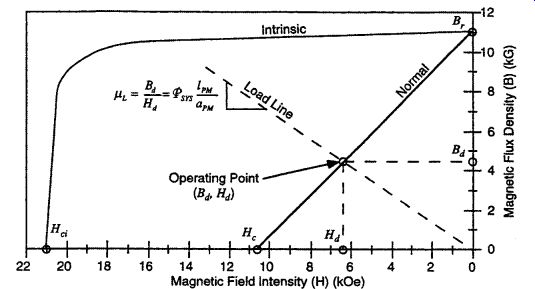
FIG. 25 Quadrant II demagnetization curves for NdFeB at 20°C, showing the operating point and the load line with no coil.

Load Line. The permanent-magnet operating point must be determined before the size and the material of the permanent magnet can be finalized. The operating point is the intersection of the permanent-magnet recoil line (in this case the normal curve) and the system load lines, as shown in Fig. 25. Since the load line passes through the operating point (Bd, Hd) and the origin (0, 0), the slope of the load line

µL can be defined as follows.

µL = (Eq. 255)

The system load line can be determined by using (Eq. 18), which states that the system magnetic flux is equal to the product of the system magnetizing force and the system permeance _sys. In a system with a permanent magnet and no coil (see Fig. 26), the system magnetizing force is proportional to the permanent-magnet field intensity Hd, and the system magnetic flux is proportional to the permanent magnet flux density Bd, as described in Eqs. (Eq. 21) and (Eq. 22).

FIG. 24 Normal demagnetization curves for several common materials.

TABLE 2 Hard Magnetic Material (Permanent-Magnet) Properties

Solving (Eq. 257) for the load-line slope results in the following definition of the load line. In some references, this slope is also called a permeance coefficient.

When a coil is added to the system, as shown in Fig. 26, (Eq. 256) is modified as follows to include the coil magnetizing force. In this case, it is assumed that the coil magnetizing force is negative, or propagates in a direction that would demagnetize the permanent magnet.

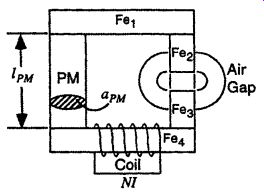
FIG. 26 Sketch of a permanent magnet in a simple system with a coil.

This load-line equation shows that the slope of the load line is independent of the coil. However, the denominator of (Eq. 262) indicates that the load line passes through both the operating point (Bd, Hd) and a point on the H axis (0,Hcoil), as shown in Fig. 27.The slope between these two points can be written as follows and equated with the result from (Eq. 262).

This shows that the H axis intercept is the magnetic field intensity of the coil as seen across the permanent magnet. This makes sense because Fig. 27 is a plot of the permanent-magnet material properties. Also, the slope of the load line represents the permeance of the system as seen across the permanent magnet.

FIG. 27 Quadrant II demagnetization curves for NdFeB at 20°C, showing the operating point and the load line with a demagnetizing coil.

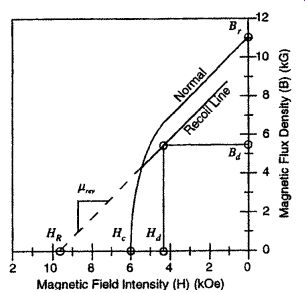
FIG. 28 Example of extending the recoil interest with the H axis.

Permanent-Magnet Reluctance Model. Magnetic systems can be modeled using electric circuit analogies, as discussed in Secs. 1.2.1 and 1.2.2. In general, from (Eq. 14), a coil is analogous to a voltage source, and the reluctance of each material and air gap in the system is analogous to a resistor. A permanent magnet can be modeled as a voltage source with a series resistance as follows.

1. The recoil line is the path of the operating point. The slope of the recoil line

µrev defines the magnetic flux density change as a function of the magnetic field intensity change. Therefore, the permanent-magnet reluctance can be defined from (Eq. 29) as follows.

_PM = (Eq. 265)

2. Extending the recoil line (beyond the normal and intrinsic curves if needed) to intersect with the H axis gives the effective coercive force of the recoil line HR, as shown in Fig. 28.The permanent-magnet magnetizing force provided at zero magnetic flux is then defined from (Eq. 22) as follows.

NIPM = HRlPM (Eq. 266)

The reluctance model for the permanent magnet is included in Fig. 29 with the entire reluctance model for the system from Fig. 26. The iron reluctance values _Fe1,_Fe2,_Fe3, and _Fe4 can be easily calculated from (Eq. 29) when the geometry and the soft magnetic properties are known. The reluctance of the air gap _air is simply the inverse of the air gap permeance. The air gap permeance can be easily calculated from the equations in Sec. 1.2.5 when the geometry of the air gap is known. The load line for the system shown in Fig. 28 can be calculated from the reluctances in Fig. 29 as follows.

The inductance of the coil in Fig. 26 can also be calculated based on the system permeance _sys and (Eq. 31), as follows.

6. LOSSES

Power losses generally take the form of hysteresis loss, eddy current loss, coil electrical resistance loss, and mechanical friction. The losses that are discussed here are the losses in the magnetic material, called core loss Pc, which includes the hysteresis loss PH and the eddy current loss PE. Data from U.S. Steel for the typical 60-Hz core loss in steel motor-lamination materials (M19 through M45) indicates that approximately 67 percent of the core loss is due to hysteresis effects and 33 per cent of the core loss is due to eddy current effects. The published core loss proper ties of magnetic materials show only the total core loss. Therefore, the hysteresis loss and the eddy current loss can be approximated as follows. The units of core loss are in power per unit mass, for example, watt per kilogram.

Total core loss PC,W/kg

6.1 Hysteresis Power Loss

The hysteresis power loss is caused by forcing the magnetic material around the hysteresis loop. Each time the magnetic domains change direction, external energy is required. As shown in Sec.

1.2.4, the area inside the hysteresis loop represents energy (Fig. 22). Each time the magnetic material is forced around the hysteresis loop, energy equal to the area inside the hysteresis loop is lost. Therefore, the hysteresis power loss is proportional to the product of the hysteresis loop area and the cyclic frequency, as shown here. The outer hysteresis loop area wH, J/m3 , can be approximated as a rectangle having a height of 2BS and a width of 2HC.

wH = 4BSHC (Eq. 275)

Dividing the hysteresis loop area by the magnetic material density ? and multi plying it by the cyclic frequency f gives the outer loop hysteresis core loss PH,W/kg, as follows.

PH = 4BSHCf (Eq. 276)

The area of a minor hysteresis loop can be approximated by substituting the peak flux density BP in place of the saturation flux density BS, and by assuming that the minor loop width remains constant.

PH = 4BPHCf (Eq. 277)

It should be noted here that the hysteresis core loss is directly proportional to the excitation frequency.

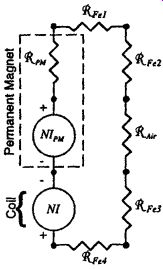
FIG. 29 Permanent magnet reluctance model for the system in Fig. 26.

6.2 Eddy Current Power Loss

Eddy currents are induced around a changing magnetic field as defined by the induced voltage from Faraday's law and the conductivity of the material. An example of a changing magnetic flux density B inducing an eddy current density Je in a magnetic steel material is shown in Fig. 30.At low frequencies, the magnetic flux density is uniform over the steel cross section T ×W. However, at high frequencies the magnetic flux moves toward a thin layer near the outer surface of the magnetic material called the skin. This is called the skin effect. The skin thickness is defined as follows, where µ is the magnetic permeability, f is the cyclic frequency,? is the radian frequency, and s is the electrical conductivity.

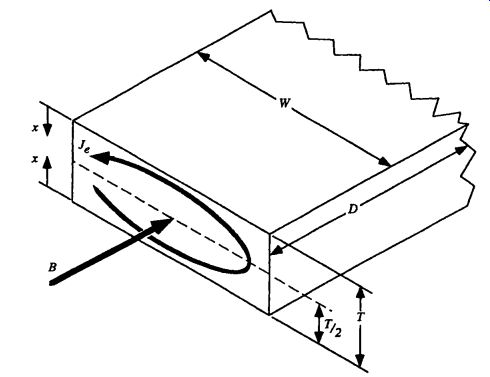
FIG. 30 Magnetic flux density B in a steel lamination induces eddy current density Je and produces an opposing magnetic flux according to Lenz's law.

Low Frequencies, No Skin Effect (T < 0.5s). The voltage induced over the length of the eddy current path is defined by Faraday's law as follows. Under the condition of T < 0.5s, it can be assumed that the magnetic flux density is uniform over the cross-sectional area of the lamination.

The number of turns made by the eddy current around the magnetic flux is one.

The magnetic flux density is applied over an area a starting at the center of the lamination, and the eddy current path length le is the distance around the magnetic flux density area. Also, it is assumed that the lamination thickness T is small compared to the width W, and the flux density is a sinusoidal function of time as follows.

Substituting Eqs. (Eq. 282) through (Eq. 287) into (Eq. 281) gives the following expression for the electric field intensity in the path of the eddy current.

The eddy current density is then obtained by multiplying the electric field intensity by the conductivity of the material in the path of the eddy current. The root mean square (RMS) value for the eddy current density is then obtained by dividing by the square root of 2, as follows.

The power loss per unit volume due to the eddy current density is equal to the square of the eddy current density RMS value divided by the conductivity.

The total eddy current power loss can be obtained by integrating over the entire volume. The eddy current power loss per unit mass (or the eddy current core loss) is obtained by dividing by the total mass of the eddy current path m =?v, as follows.

The differential volume of the eddy current path and the total volume are defined from Fig. 30 as follows.

Substituting Eqs. (Eq. 290), (Eq. 292), and (Eq. 293) into (Eq. 291) gives the following expression for the eddy current core loss:

where T < 0.5s.

It should be noted here that the eddy current core loss is directly proportional to the square of the excitation frequency, the square of the flux density, and the square of the lamination thickness.

High Frequencies, Large Skin Effect (T > 5.0s). Under the condition of T > 5.0s, the magnetic flux density is not uniform over the cross-sectional area of the lamination. According to Bozorth (1993), it can be assumed that magnetic flux density varies exponentially over the cross-sectional area as follows.

Substituting (Eq. 298) into (Eq. 281) and following the process previously used for Eqs. (Eq. 288) through (Eq. 297) gives the following general expression for the eddy current core loss.

The eddy current core loss equation (Eq. 300) is asymptotic to the following two limiting equations.

As can be seen from (Eq. 298), the magnetic flux is not completely confined to the depth of one skin thickness. However, Steinmetz defined a depth of penetration d which is described in Roters (1941) and Bozorth as the required surface layer thickness that will contain all of the magnetic flux at a uniform magnetic flux density equal to the magnetic flux density at the outside surface. The depth of penetration is shown in (Eq. 303).

d = d = (Eq. 303)

Comparing the skin depth s in (Eq. 278) to the depth of penetration d in (Eq. 303) gives the following relationship.

The depth of penetration d can be used to determine the total effective magnetic flux cross-sectional area and the peak magnetic flux density at the surface. This provides the capability to consider the effects due to saturation on performance, such as determining the limitations on peak force and peak inductance.

6.3 Reflected Core Loss Resistance

The core loss of an electromagnetic device can be modeled as a reflected resistance in the coil or as a wider hysteresis loop. The reflected core loss resistance RC in the coil can be calculated by considering the total power loss in the core PC?v and the power loss of the coil I2 R as follows, where PC is the core loss, W/kg; ? is the density, kg/m^3; and v is the volume,m^3.

6.4 Imaginary Permeability

As described in Sec. 6.1, the hysteresis loop area represents an energy loss. Also, for non-saturating conditions, the hysteresis loop can be modeled as a rotating vector system based on (Eq. 23) as follows.

B =µH = (µR + jµi)H (Eq. 309)

The system inductance and impedance can be written based on equations [1-30], [1-31] and [1-308].

The first term of (Eq. 312) represents the resistive impedance, and the second term represents the reactive impedance. Therefore, only the first term contributes to the power loss, as shown in (Eq. 313).

The first term of (Eq. 313) represents the power loss in the coil resistance, and the second term represents the power loss in the core. Therefore, the second term can be equated with the power loss in the core from (Eq. 306), and the imaginary permeability can be determined, as follows.

(Eq. 22) can be written for NI, (Eq. 23) can be written for H, and volume of the core is simply the product of the magnetic flux path length and the magnetic flux cross-sectional area. Substitution of these relations into (Eq. 315) gives the imaginary permeability as a function of the excitation (B, ?) and the material properties (Pc, ?, µ).

7. MAGNETIC MOMENT (OR MAGNETIC DIPOLE MOMENT)

This section describes the magnetic moment and its use in determining the proper ties of magnetic materials. The magnetic moment (which is based on a current loop) can be used to model the field around a permanent magnet. Correlations for approximately the magnetic field distribution for a magnetic moment and for a current loop are also presented in this section.

The properties of a magnetic material are described based on magnetization curves, which can be presented in a number of different ways, as listed here. These properties and their relationship to the atomic magnetic moment (Bohr magneton) are explained in this section.

_ Total or normal flux density B versus magnetizing force H

_ Intrinsic flux density Bi, µ0M, 4pM, 4pI, or 4pJ versus magnetizing force H

_ Magnetic moment m versus magnetizing force H

_ Magnetic moment per unit volume m/V versus magnetizing force H

_ Magnetic polarization M, I, or J versus magnetizing force H

7.1 Magnetic Moment for a Current Loop

The magnitude of the magnetic moment m for a current loop is equal to the loop area pa^2 times the current I (see Fig. 31). The direction of the magnetic moment m is in the direction of the thumb as the fingers of the right hand follow the current I.

m =pa2 I A·m2 or J/T (Eq. 321)

7.2 Magnetic Moment for a Magnetic Material

The magnetic moment m for a permanent magnet is equal to the magnetization M times the volume V, with a direction perpendicular to the north pole face (see Fig. 32).The magnetization or magnetic polarization M of a permanent magnet is equal to the operating point intrinsic flux density Bdi (see Fig. 33) divided by the permeability of free space µ0 = 4p× 10^-7 (T·m)/A or H/m.

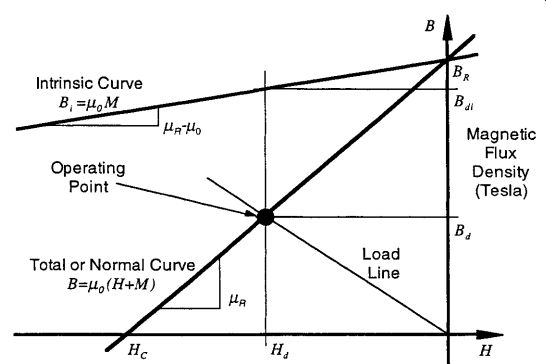
FIG. 33 Quadrant II permanent magnet demagnetizing curve.

Approximate Magnetic Moment for a Permanent Magnet. High-energy permanent magnets (such as NdFeB and SmCo) typically have a very small recoil permeability µR, so that µR ˜µ0. Therefore, the magnetic polarization M and the magnetic moment m can be approximated as follows.

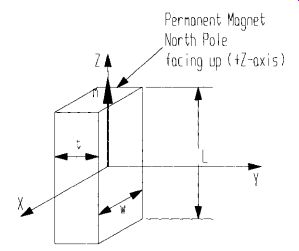
FIG. 32 Magnetic moment for a permanent magnet.

Permanent Magnet Current Loop Model. A high-energy permanent magnet can be modeled as a current loop by equating the magnetic moments as follows, where Hc is coercive force. This is 99.99 percent accurate for short magnets with high coercive force (NdFeB or SmCo), and 70 percent accurate for long magnets with low coercive force (alnico).

Permanent Magnet Pole Strength and Dipole Model. The magnetic dipole moment m can also be written as the product of the magnetic pole strength p and the distance l between the poles. The magnetic pole strength p of a high-energy permanent magnet can be approximated by the product of the coercive force Hc and the pole face area wt.

FIG. 34 Torque on a magnetic moment in a uniform magnetic field.

7.3 Torque on a Magnetic Moment in a Uniform Field

Torque T is produced on a magnetic dipole moment m by a uniform magnetic field B (see Fig. 34). The torque is in the direction to align the magnetic moment with the direction of the uniform magnetic field.

7.4 Magnetic Moment in Atoms (Bohr Magneton)

The magnetic moment in various types of materials is a result of the following factors.

_ Electron orbit. An electron in an orbit around a nucleus is analogous to a small current loop, in which the current is opposite to the direction of electron travel.

This factor is significant only for diamagnetic and paramagnetic materials, where it is the same order of magnitude as the electron spin magnetic moment.

The magnetic properties of most materials (diamagnetic, paramagnetic, and antiferromagnetic) are so weak that they are commonly considered to be non magnetic.

_ Electron spin. The electron cannot be accurately modeled as a small current loop. However, relativistic quantum theory predicts a value for the spin magnetic moment (or Bohr magneton ß) as shown following in (Eq. 344). In an atom with many electrons, only the spin of electrons in shells which are not completely filled contribute to the magnetic moment. This factor is at least an order of magnitude larger than the electron orbit magnetic moment for ferromagnetic, antiferromagnetic, and super-paramagnetic materials.

Bohr magneton (spin magnetic moment)

Mass of an electron me = 9.1094 × 10^-31 kg

_ Nuclear spin. This factor is insignificant relative to the overall magnetic proper ties of materials. However, it is the basis for nuclear magnetic resonance imaging (MRI).

_ Exchange force. The exchange force is an interaction force (or coupling) between the spins of neighboring electrons. This is a quantum effect related to the indistinguish-ability of electrons, so that nothing changes if the two electrons change places. The exchange force can be positive or negative, and in some materials the net spins of neighboring atoms are strongly coupled.

Chromium and manganese (in which each atom is strongly magnetic) have a strong negative exchange coupling, which forces the electron spins of neighboring atoms to be in opposite directions and results in antiferromagnetic (very weak) magnetic properties. Iron, cobalt, and nickel have unbalanced electron spins (so that each atom is strongly magnetic) and have a strong positive exchange coupling. Therefore, the spins of neighboring atoms point in the same direction and produce a large macroscopic magnetization. This large-scale atomic cooperation is called ferromagnetism.

7.5 Intrinsic Saturation Flux Density

The theoretical intrinsic saturation flux density for iron, nickel, and cobalt can be calculated using (Eq. 345) as follows. Typically, the intrinsic saturation flux density Bi is measured and the number of Bohr magnetons per atom n0 is calculated.

The ferromagnetic properties of materials disappear when the temperature becomes high enough. This temperature is called the Curie temperature Tc or the Curie point. Iron (Tc = 770°C), nickel (Tc = 358°C), and cobalt (Tc = 1130°C) are the only ferromagnetic materials that have Curie points above room temperature.

Some rare earth metals like gadolinium (Tc = 16°C), dysprosium (Tc =-168°C), and holmium are ferromagnetic, but their Curie points are below room tempera ture.

Theoretical intrinsic saturation flux density Bi, T

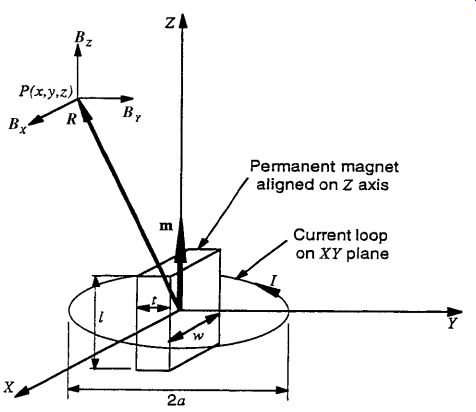
FIG. 35 Geometric configuration for a magnetic dipole moment.

7.6 Magnetic Far Field for a Magnetic Dipole Moment

The magnetic field is well defined for points far from a magnetic dipole moment (far field, R _ a; see Fig. 35).This means that the distance R must be large compared to the size of the magnetic dipole radius a or length l, or the size of the magnetic dipole a or l must be small compared to the distance R:

8. MAGNETIC FIELD FOR A CURRENT LOOP

The magnetic field produced by a moving charge can be calculated by the Biot Savart law. Integrating the Biot-Savart law over a current path gives the total magnetic field produced by the entire current path. This technique can be used to determine the magnetic field produced by a current loop, such as a single-turn wire loop or a magnetic moment. Further integration of the magnetic field over the area of the wire loop gives the inductance.

8.1 Biot-Savart Law

The Biot-Savart law gives the exact field distribution (in the absence of magnetic materials) for both the near and far fields, for any current path, or for any current path segment. The Biot-Savart law as applied to a circular wire loop in the XY plane is shown in Fig. 36 (Note that Eqs. (Eq. 346) to (Eq. 348) may be used to approximate the far field, R _ a).

8.2 Axial Field (Bz).

The Biot-Savart equation (Eq. 350) can be easily integrated to obtain the axial (Z axis) magnetic field Bz (x = 0, y = 0, R = z).

8.3 Approximate Axial Field Bz, Based on a Parallel Straight Wire Assumption

The magnetic field on the XY plane (z = 0,R = a) can be very roughly approximated on the field between two parallel straight wires as follows.

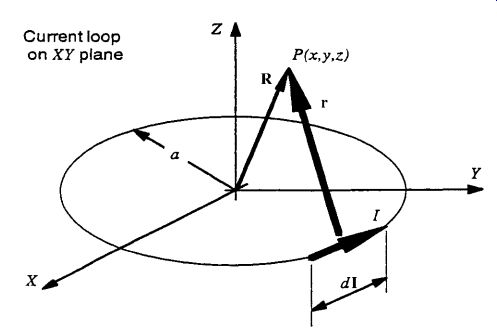
FIG. 36 Geometric configuration for the Biot-Savart law.

8.4 Inductance for a Single-Turn Wire Loop

The following approximation for the inductance of a single-turn wire loop is very accurate for small wires (a/r0 > 10), from Plonsey and Collin (1961) (r0 = wire radius).The classical solution (which involves elliptic integrals) is required when the wire is large.

8.5 Approximate Inductance Based on a Parallel Straight Wire Assumption

The inductance of a single-turn wire loop can be very roughly approximated (based on the field between two parallel straight wires) by integrating (Eq. 356) over the area of the loop and dividing by the current, as follows, where r = wire radius:

Error < 8.6 percent for a/r0 > 3.

The error in (Eq. 360) relative to the Plonsey and Collin approximation (Eq. 358) ranges from +5.3 percent at a/r0 = 3 to -8.6 percent at a/r0 = 13, and falls off to -4.5 percent at a/r0 = 1000. The + indicates that (Eq. 360) gives a larger value than (Eq. 358), and the - indicates that (Eq. 360) gives a smaller value than (Eq. 358).

9. HELMHOLTZ COIL

The Helmholtz coil (Fig. 37) is a pair of identical coils with a mean coil axial separation equal to the mean coil radius a, where the resulting axial magnetic field BZ is uniform within 10 percent inside a sphere of radius 0.1a located midway between the two coils, z = a/2. The best performance is obtained when both the width w and the thickness t of the winding cross section are less than 20 percent of the mean radius.

The first, second, and third derivatives of the axial field dn BZ/dzn (n = 1, 2, 3) are all equal to zero at z = a/2.

The axial field BZ at the midpoint z between the two coils (z = a/2) can be obtained by doubling the field from (Eq. 352), where NI = the amp-turns in each coil.

10. COIL DESIGN

AC and dc coils need to be designed differently to function properly. Some of the common terms relating to both types of coils are defined here. The electrical conductivity s of copper is defined at a temperature of 20°C (s20). Copper also has a

temperature coefficient of resistance a. As a coil gets hot, its electrical resistance increases. The electrical conductivity at temperatures other then 20°C can be calculated as follows.

Copper conductivity at 20°C

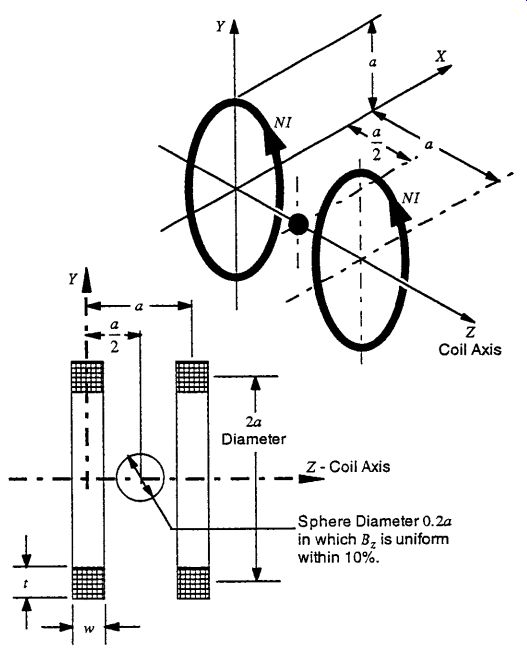
FIG. 37 Helmholtz coil configuration: two identical coils in the XY plane, with radius a, and with an axial separation a equal to the radius.

The bare copper wire diameter dB can be used to determine the resistance of a coil. The bare wire diameter is a function of the American Wire Gauge (AWG) number as follows, where the bare wire diameter d0 for AWG = 0 is 0.00826 m = 0.325 in.

dB = d0 (Eq. 123-AWG) d0 = 0.00826 m (Eq. 369) The total wire diameter includes the thickness of the electrical insulation layer (usually a varnish coating) and is used to determine the coil size or the number of turns that will fit on a bobbin. The wire insulation thickness is specified by the number of insulation layers that are built up on the wire, such as single build and double build. The total insulated wire diameter can be calculated based on a curve fit of the tables from MWS Wire Industries (1985), as follows. These equations give the total insulated wire diameter in units of meters and are accurate to within ±4 percent over the wire size range of AWG 4 to 60.

The typical winding density n for a given wire can be calculated based on a square lay, assuming each wire uses a square region equal to its diameter. Coils are usually wound with much less precision, so a winding density factor C is included to account for voids caused by loose windings or terminations. The winding density factor typically varies from 0.70 up to 0.95, and has units of turns per unit cross-sectional area.

n = C (Eq. 374)

The maximum winding density can be achieved if the wires form a triangular or a hexagonal cross-section pattern. The maximum winding density nmax and the corresponding maximum winding density factor Cmax are shown here.

The geometry of the bobbin is shown in Fig. 38. The bobbin length l, outside diameter D0, and inside diameter DI are used to determine the mean turn length lM and the winding cross-sectional area AW.

Mean turn length lM =p (Eq. 377)

Winding cross-sectional area AW = l (Eq. 378)

10.1 DC Coil

The typical requirement in a dc coil design is to determine the turns N, the wire size AWG, the temperature rise ?T, the coil resistance R, and the inductance L, given the required amp-turns NI. The required amp-turns can be obtained from (Eq. 17) by knowing the required magnetic flux f and the system reluctance _sys.

The first thing that should be done is to estimate the maximum temperature of the coil, or the maximum allowable temperature unit. Then calculate the copper conductivity at the elevated temperature. Use of the elevated temperature conductivity will guarantee that the coil will provide the required amp-turns at the maximum temperature. The resistance of the coil can be determined by dividing the length of the wire by the conductivity of the wire and by the cross-sectional area of the wire aB =pd2 B/4,

as follows.

The electrical current in the coil can be calculated by solving Ohm's law for the current. Multiplying by the number of turns in the winding gives the amp-turns produced by the coil.

I = (Eq. 380) NI = N (Eq. 381) where I = amperes V = volts R = ohms

Substitution of (Eq. 379) into (Eq. 381) gives the following equation, which can be solved for the bare wire diameter. Note that in (Eq. 382) the coil NI is independent of the number of turns N. This is true as long as any change in the number of turns does not significantly change the mean turn length lM.

FIG. 38 Cylindrical bobbin dimensions for coil winding.

The bare wire diameter must be larger than or equal to the expression on the right of (Eq. 383) to guarantee that the minimum coil NI is at least as large as the required NI. (Eq. 369) can be written to solve for the AWG wire size, as follows. The AWG sizes are typically in integer increments; therefore, only the rounded-down integer value of the expression is useful in this case. AWG wire sizes are available in half-gauge increments, but in small quantities they are 2 to 3 times more expensive. Note that the AWG number is dimensionless and that both d0 and dB must have the same units:

AWG = int

__ (Eq. 384)

where d0 = 0.00826 m = 0.325 in.

Now that the AWG wire size is determined, the actual bare wire diameter can be obtained from (Eq. 369), and the total wire diameter can be obtained from Eqs.

(Eq. 370) through (Eq. 373).The total number of turns that will fit on the bobbin can be calculated by using Eqs. (Eq. 374) and (Eq. 378).

N = nAW = (Eq. 385)

The coil resistance can be obtained from (Eq. 379), the coil inductance can be obtained from (Eq. 31), and the coil current can be obtained from Ohm's law. The power dissipation at the elevated temperature can be calculated as follows.

Q = W (Eq. 386)

The steady-state temperature rise of the coil can be determined as shown here, where h is the combined heat transfer coefficient for convection and radiation, A is the heat transfer surface area of the coil, and ?T is temperature rise above the ambient temperature.

10.2 AC Coil

The typical requirement in an ac coil design is to determine the turns N, the wire size AWG, the temperature rise ?T, the coil resistance R, and the inductance L, given the required magnetic flux f. The performance of an ac coil is defined by Ohm's law and Faraday's law.

Equations (Eq. 369) through (Eq. 373) were curve-fit to a single expression for the total wire diameter. These equations can be written to solve for the AWG wire size, as was done in (Eq. 384), and as shown here for single-build insulation, (Eq. 401).

The AWG wire sizes are in integer increments; therefore, only the rounded-up integer value of the expression is useful in this case. Note that this equation uses the wire diameter in units of meters.

With the AWG wire size determined, the actual bare wire diameter can be obtained from (Eq. 369), the total wire diameter can be obtained from Eqs. (Eq. 370) through (Eq. 373), and the coil resistance can be obtained from (Eq. 379).

With the coil resistance defined, the actual peak magnetic flux fA can be deter mined from (Eq. 402), for the condition when the coil resistive impedance is significant.

If the actual magnetic flux is less than the required magnetic flux (fA <fP), then the number of turns N must be reduced, and the calculation procedure should return to (Eq. 400) to obtain a new wire diameter based on the new number of turns. This procedure should continue until the actual peak magnetic flux is approximately equal to the required peak magnetic flux (fA ˜fP), within an acceptable tolerance.

If fA ˜fP, then the procedure should continue as follows. The coil inductance L can be obtained from (Eq. 31), and the coil impedance Z and the coil current I can be determined as follows.

The power dissipation at the elevated temperature can be calculated as follows, and the coil temperature rise can be obtained from Eqs. (Eq. 387) through (Eq. 391).

10.3 Copper Area Ratio Approximation

The wire diameter equations Eqs. (Eq. 370) to (Eq. 373) can be simplified based on the estimated copper area ratio KA. The copper area ratio is defined in (Eq. 407) as follows, where AC is the copper cross-sectional area and AW is the total winding cross sectional area from (Eq. 378).

With a winding density factor C of 0.70, the following values of the copper area ratio KA can be used. A winding density factor of 0.70 is conservative, because most coils can be wound with a higher winding density. Therefore, a coil designed with this approximation will be manufacturable.

The copper cross-sectional area can be obtained by rewriting (Eq. 407) and including the effect of different values for the winding density factor, as follows.

The copper cross-sectional area can also be calculated from the number of turns N and the bare wire diameter dB, as follows.

Equations (Eq. 408) and (Eq. 409) can be combined to determine the number of turns or to determine the bare wire diameter. In the case of a dc coil design, the number of turns N can be determined from (Eq. 410) without needing to use the set of diameter equations Eqs. (Eq. 370) to (Eq. 373) and (Eq. 385). In the case of an ac coil design, the bare wire diameter dB can be determined from (Eq. 411) without needing to use (Eq. 400), the set of diameter equations Eqs. (Eq. 370) to (Eq. 373), and (Eq. 401).

Approximate number of turns for dc coils

Approximate maximum bare wire diameter for ac coils

10.4 Coil Design Procedures Using the Copper Area Ratio Approximation

The equations given previously in Sec. 10 for the coil geometry, dc coil performance, ac coil performance, and copper area ratio are listed in the following two subsections. These general design procedures for dc and ac coils will determine the wire size, the number of turns, and the coil performance from the known coil voltage, bobbin geometry, and required magnetic performance NI or f.

DC Coil Design Procedure

1. Given:

Coil dc voltage V

11. RELUCTANCE ACTUATOR STATIC AND DYNAMIC (MOTION) ANALYSIS

As shown in Figs. 2 and 29, the electrical analogy of the magnetomotive force supplied by a coil is an electrical voltage source, and the electrical analog for the reluctance of the steel part and the air gaps is an electrical resistor. Analysis of the reluctance actuator shown in Fig. 39 is based on reluctance circuits that correspond to the electrical analogy. Section 1.11.1 shows the static dc steady-state analysis and Sec. 1.11.2 shows the dynamic analysis with time-varying coil voltage and armature motion.

11.1 Static Analysis (DC, Steady State)

The reluctance circuit for the system in Fig. 39 can be solved by writing the equation for each flux loop, based on (Eq. 14). In general, the magnetomotive forces around each loop are summed to zero, _ NI = 0.This results in two flux-loop equations with two unknowns. The circuit elements and the loop equations for both of the flux loops are listed here.

_A = reluctance of the steel armature

_g = reluctance of the air gap between the armature and the magnet pole

_L = reluctance of the leakage air path between the vertical legs of the magnet pole

_H = reluctance of a vertical leg of the steel magnet pole

_W = reluctance of the bottom of the steel magnet pole

FIG. 39 (a) Example of a reluctance actuator in which only one coil is used, and (b) the corresponding reluctancy circuit.

The reluctances for the actuator in Fig. 39 can be easily calculated from (Eq. 29) and (Eq. 116) through (Eq. 163), and the coil current I can be calculated by dividing the dc source voltage V by the coil resistance R. These equations can then be solved for the loop fluxes as follows.

The system reluctance defined in (Eq. 418) can be used to calculate the inductance of the coil from (Eq. 31), and if a permanent magnet replaces the coil, a load line can be calculated from (Eq. 269) as follows.

The force on the armature can be calculated from (Eq. 74) by determining the magnetizing force across the air gap as follows. The system in Fig. 39 does not have an armature coil; therefore, Na = 0.

11.2 Dynamic Analysis (AC and Motion)

The force in (Eq. 424) is valid for steady-state dc current with no armature motion.

If a transient solution is required, or if the source voltage is a function of time (such as ac voltage), or if the armature is allowed to move, then the coil voltage must be defined using both Ohm's law and Faraday's law. (Eq. 417) is also used as the definition of magnetic flux for this system.

The time derivatives of the coil turns N and the system permeance _sys in (Eq. 424) can be expanded as a function of the armature position X and the armature velocity v by using the chain rule as follows.

Substitution of (Eq. 428) and (Eq. 429) into (Eq. 426) gives the general form of the coil equation.

The second term can be written using the inductance definition, (Eq. 31), and the fourth term can be written using the permeance definition, (Eq. 419), to pro vide a more familiar appearance, as follows.

The first term represents the resistance voltage drop, the second term represents the inductive voltage drop, the third term represents the voltage drop produced by the armature velocity and by changing reluctance, and the fourth term represents the voltage drop produced by the armature velocity and by the change in the number of turns that link the magnetic flux. Both the third term and the fourth term contain the armature velocity and are usually referred to as the back electromotive force (emf). The coil in the system shown in Fig. 42 (see Sec. 1.12) has a constant number of turns linking the flux. Therefore, the fourth term can be ignored. The resulting voltage equation can be written as follows.

(Eq. 433) can be solved for the current I, and the magnetic flux f1 can be obtained by solving (Eq. 419) based on the coil current. (Eq. 433) describes the time-varying coil current I as a function of the known variables (the voltage, the system permeance, the number of turns in the coil, the armature velocity, and the coil resistance). (Eq. 433) also shows that the coil current is a function of the armature velocity.

An alternative solution method for this system is to substitute (Eq. 419) into (Eq. 425), and then rearrange the terms as follows to solve for the magnetic flux.

(Eq. 437) can be solved for the magnetic flux f1, and the coil current can be obtained by solving (Eq. 419) based on the magnetic flux. (Eq. 437) describes the time-varying magnetic flux f1 as a function of the known variables (the coil voltage, the system permeance, the number of turns in the coil, and the coil resistance), and it shows that the magnetic flux is not a function of the armature velocity.

(Eq. 438) shows that the dc steady-state solution is identical to (Eq. 420).

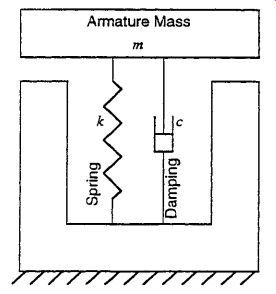
FIG. 40 Reluctance actuator mass, spring, and damping dynamic system.

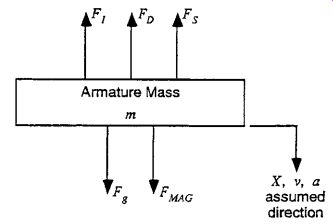
FIG. 41 Reluctance actuator armature free-body diagram.

11.3 Mechanical Dynamics

The armature velocity and position can be determined by solving the dynamic sys tem shown in Figs. 1.40 and 1.41.Where F mag is the magnetic force from (Eq. 424), Fg is the force due to gravity, FI is the inertia force in opposition to the acceleration a, FD is the damping force in opposition to the velocity v, Fs is the spring force in opposition to the displacement or position X, and F0 is the initial spring force.

Force balance

The performance of this actuator can be calculated by solving the differential equation for the coil current I, (Eq. 433), or the differential equation for the magnetic flux f1, (Eq. 437), and the differential equation for motion, (Eq. 444). Equations (Eq. 419), (Eq. 415), and (Eq. 424) are needed to solve for the other variables, f1 or I, f2, and Fmag. Equations (Eq. 433) and (Eq. 437) are first-order nonlinear differential equations, and the system permeance and the armature velocity are functions of the armature position and the armature force. Therefore, this set of equations must be solved with an iterative finite-difference technique, such as fourth-order Runge-Kutta.

FIG. 42 (a) A moving-coil actuator in which the field coil is stationary and the armature coil moves. This shape of this actuator is cylindrical. (b) The corresponding reluctance circuit.

12. MOVING-COIL ACTUATOR STATIC AND DYNAMIC (MOTION) ANALYSIS

Analysis of the moving-coil actuator shown in Fig. 42 is based on reluctance circuits that correspond to the electrical analogy. Section 12.1 shows the static dc steady-state analysis and Sec. 12.2 shows the dynamic analysis with time-varying coil voltage and armature motion.

12.1 Static Analysis (DC, Steady State)

The reluctance circuit for the system in Fig. 42 can be solved by writing the equation for each flux loop, based on (Eq. 14). In general, the magnetomotive forces around each loop are summed to zero, _ NI = 0.This results in two flux-loop equations with two unknowns. The circuit elements and the loop equations for both of the flux loops are listed here.

_g = reluctance of the air gap between the center pole and the outer pole

_L = reluctance of the leakage air path between the center pole and the outer pole

_C = reluctance of the center steel magnet pole

_H = reluctance of the outer steel magnet pole

_W = reluctance of the bottom of the steel magnet pole

NaIa = magnetomotive force of the moving armature coil

NfIf = magnetomotive force of the stationary field coil

Both of the coils and the magnet pole are cylindrical. Therefore, the outer legs of the magnet pole are one piece of steel in the shape of a tube. The reluctance circuit in Fig. 42 is shown with the coils on the center pole and only one reluctance value

_H for the outer tubular pole. Equations (Eq. 445) and (Eq. 446) can be solved for the second loop magnetic flux f2 as follows.

The system reluctance defined in (Eq. 461) can be used to calculate the inductance of the moving armature coil from (Eq. 31), as follows.

The force on the armature can be calculated from (Eq. 203).The system in Fig. 42 does not have a moving magnetic armature; therefore, the permeance of the working gap _g is constant. Also, Ia, If, and Nf are assumed to be constant.

The rate of change of the moving coil turns with respect to the armature position is simply the number of turns in the coil Na divided by the coil length la. Also, the total length of the wire in the air gap lwire is equal to the product of the wire path circumference and the number of turns in the gap, as shown following. At this point it

is assumed that all of the air gap flux exists in the direct face-to-face interface (no fringing flux).This assumption is valid for small air gaps, where g _ pDTA.

12.2 Dynamic Analysis (AC and Motion)

The force in (Eq. 461) is valid for steady-state dc current with no armature motion and for small air gaps, where g _ pDTA.

If a transient solution is required, or if the armature is allowed to move, then the current in the moving coil must be defined with both Ohm's law and Faraday's law, (Eq. 16) and (Eq. 20), as follows. In this derivation, the field coil is assumed to have a constant current and a constant number of turns. The permeance of the working air gap is also assumed to be constant.

Substitution of Eqs. (Eq. 428), (Eq. 457), (Eq. 459), and (Eq. 460) into (Eq. 465) gives the following result for the voltage on the moving armature coil.

Va = IaRa + La +ffv + 2fav (Eq. 466)

The first term represents the resistance voltage drop, the second term represents the inductive voltage drop, the third term represents the voltage drop produced by the velocity of the armature coil as it passes through the field produced by the field coil, and the fourth term represents the voltage drop produced by the velocity of the armature coil as it passes though the field produced by itself (this is an armature reaction voltage). Both the third term and the fourth term contain the armature velocity and are usually referred to as the back emf. (Eq. 465) can be written as follows.

(Eq. 467) can be solved for the current Ia, and the magnetic flux f2 can be obtained by solving (Eq. 453) based on the coil current. (Eq. 467) describes the time-varying coil current I as a function of the known variables (the coil voltage, the system permeance, the number of turns in each coil, the current in the bias field coil, the armature velocity, and the coil resistance). (Eq. 467) also shows that the coil current is a function of the armature velocity.

An alternative solution method for this system is to solve (Eq. 452) for the coil current Ia, substitute the result into (Eq. 462), and then rearrange the terms as follows to solve for the magnetic flux.

(Eq. 472) describes the magnetic flux f2 as a function of the known variables (the coil voltage, the system permeance, the number of turns in each coil, the current in the bias field coil, the armature velocity, and the coil resistance). (Eq. 472) also shows that the magnetic flux is a function of the armature velocity.

The performance of the system shown in Fig. 42 can be calculated by solving the differential equation for the coil current I4, (Eq. 467), or the differential equation for the magnetic flux f2, (Eq. 472). In either case, Eqs. (Eq. 452), (Eq. 447), (Eq. 461), (Eq. 440), (Eq. 441), and (Eq. 442) are needed to solve for the other variables, f2 or Ia, f1, Fmag, a, v, and X.

The armature velocity and position can be calculated by solving the mechanical dynamic equations listed earlier in Eqs. (Eq. 439) to (Eq. 442). Equations (Eq. 467) and (Eq. 472) are first-order nonlinear differential equations. The number of turns on the moving armature coil that link the air gap flux and the armature velocity are functions of the armature position and the armature force. Therefore, the best way to solve this equation is to use an iterative finite-difference technique, such as fourth order Runge-Kutta.

FIG. 43 shows a block diagram for the control of this moving-coil actuator. In general, a reference position Xref is input to the control and compared to the measured position Xm. The difference between the reference and measured positions is converted to a coil voltage Va by the transfer function G(s), and the actual position X is converted into the measured position by the transfer function Hm(s). KD is the mechanical damping constant of the actuator, and represents friction, bearings, oil viscosity, and air movement (wind resistance).The other two constants, KF and Kemf, are obtained directly from Eqs. (Eq. 455) and (Eq. 466), as follows.

Average turns per unit length over the entire coil

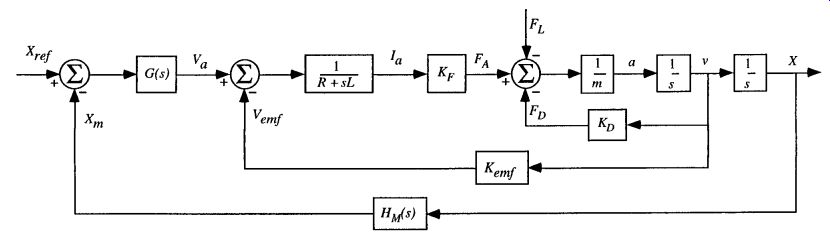
FIG. 43 Block diagram for moving-coil actuator.

13. ELECTROMAGNETIC FORCES

A force is exerted on a conductor if it is carrying current and is placed in a magnetic field. Fig. 44 shows the direction of the force when a current I flows through the conductor in the direction shown. The force F on the conductor is as follows.

F = BIl (Eq. 480) where B = flux density l = length of conductor being linked by flux I = current in conductor Torque T may be produced electromagnetically if current-carrying conductors are arranged such that they may pivot on an axis that is centered in a magnetic field, as shown in Fig. 45.

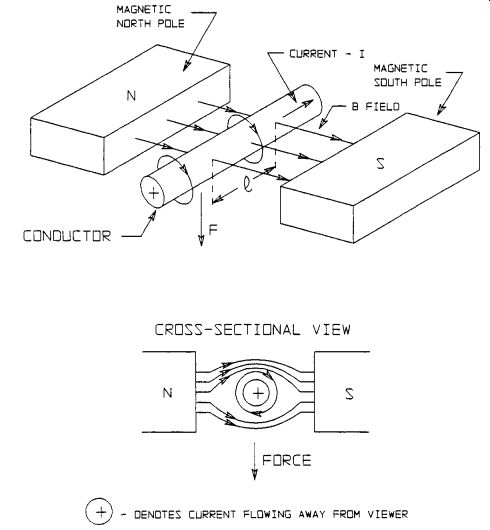
FIG. 44 Force on a conductor.

The flux in the gap between the magnetic north and south poles will interact with the flux produced by the current in the conductors. If the current is in the direction indicated in Fig. 45, the conductors will tend to rotate in the direction shown.

The following equation is used to determine the torque produced.

Where

N = number of current carrying conductors

f= flux per pole

P = number of poles

a = number of parallel current paths

I = current in the conductors

K = constant

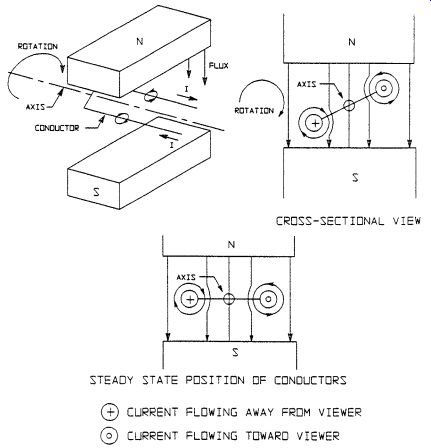
FIG. 45 Electromagnetic torque.

The bottom drawing in Fig. 45 shows the resting position of the conductors. If the direction of the current is switched as the conductors reach this position, the conductors will continue to rotate on the axis in the same direction. Commutation is the process of switching the directions of the currents to allow for continuous rotation.

In motors, the conductors are contained by magnetic steel teeth. The motor field sets up flux through these teeth. The current in the conductors causes the field to distort, setting up a net torque. The steel increases the amount of flux available to pro duce torque by lowering the circuit reluctance.

An electric motor is a device for converting electrical power to mechanical power (usually rotational).

14. ENERGY APPROACH (ENERGY-COENERGY)

Another approach to determining forces and torque is through energy concepts. The principle of conservation is the basis for the application of the energy approach.

This section considers the idea of changes in stored field energy. As an introduction to the concept, consider a magnet core, as shown in Fig. 46, around which a winding has been placed. This is a single-energy-source system since only one input is involved and no mechanical movement occurs.

Around the loop, Kirchoff's voltage law suggests (Eq. 482):

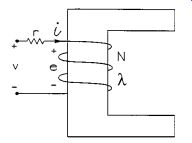
FIG. 46 Magnetic core single-energy source system.

..where vi is the instantaneous electrical power input. Integrating the energy expression yields the following:

If the system is linear without saturation, it is obvious that Wf = W' f.

The slopes of the characteristic are as follows:

= and = L (Eq. 491) where _ and L are the reluctance and inductance of the system, respectively.

Suppose we now add an armature to Fig. 46 and redraw the coil so that an air gap exists as shown in Fig. 49.

Note that under this assumption mechanical motion is involved in the coil current i and the position of the armature x, that is, ?=?(i, x).

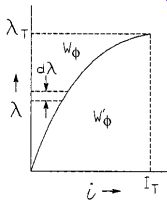
FIG. 47 Flux linkage versus current.

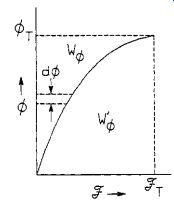
FIG. 48 Flux versus magnetizing force.

Since mechanical motion is involved, an additional equation involving Newton's law of motion is required to describe the dynamics of the system.

Before we pursue this analysis, it is very

informative to look at a graphical analysis which will give insight to the energy approach.

As previously shown, for the case in which the flux linkage is a function of the coil current i, only a two-dimensional plot is drawn (Fig. 46).However, because such a plot requires three dimensions, if we use a two-dimensional plot we now have a choice of considering constant current or constant flux linkage, giving a graphical approach to assist in understanding the energy principles. In either case, our interest is in looking at changes in energy for an energy balance.

Let us first assume we will excite the coil shown in Fig. 49 with a constant current source of magnitude i. Refer to Fig. 50 and note that five distinct areas are shown. Before the armature movement, the stored field energy area in Fig. 50 was C + D. If the armature now moves from x0 to x0 +?x, the air gap decreases and a differential change in flux and flux linkage occurs. The additional energy sup plied by the electrical circuit is as follows:

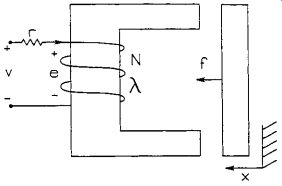
FIG. 49 Electromagnetic actuator.

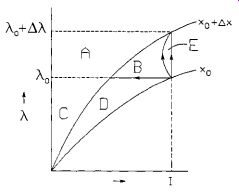
FIG. 50 Energy areas before and after movement.